1 Introduction

Electroencephalography (EEG) is a non-invasive, fast, and inexpensive method to record electrical potentials on the head surface. In neuroscience, it is important to characterize the sources of measured EEG signals and accurately localize them by solving an EEG inverse problem. The EEG inverse problem includes an EEG forward problem using a chosen source model (Grech et al., 2008; Güllmar et al., 2010; de Munck et al., 2017). The solution of the EEG forward problem yields an accurate calculation of the electromagnetic fields. To solve the EEG forward problem, the conductivity profile of the head is modeled, and the relation between the source model and the computed EEG signals is introduced in the EEG lead-field matrix, which can then be used to solve the EEG inverse problem. Then, the source locations and strengths are estimated from the measured EEG signals with the help of the EEG lead-field matrix obtained in the EEG forward model (Hallez et al., 2007; Akalin Acar and Makeig, 2013; de Munck et al., 2017; Vorwerk et al., 2017). Consequently, appropriate modeling of the EEG forward problem is an essential prerequisite for the accurate solution of the EEG inverse problem (Güllmar et al., 2010; Akalin Acar and Makeig, 2013). In other words, the physics of the problem is in the forward model, and errors caused by an inaccurate forward model cannot be corrected while solving the inverse problem.

Two advanced numerical methods called Finite Element Method (FEM) (de Munck et al., 2017; Vorwerk et al., 2017) and Boundary Element Method (BEM) (Stenroos and Sarvas, 2012; de Munck et al., 2017; Rahmouni et al., 2017) are widely used to solve the EEG forward problem. In the FEM, the entire volume is discretized into small elements (tetrahedral elements), and the potentials of all nodes are calculated. The FEM can easily incorporate arbitrary geometries and heterogeneous and anisotropic electrical conductivity of the head tissues (Wolters et al., 2006; Zhang et al., 2014; Beltrachini, 2019a). Unfortunately, the difficulty thorough using FEM is that it causes singularity when using the point dipoles as current dipoles in the EEG forward model, which increases the error of forward solution. However, the current dipoles are widely accepted models for modeling neuronal activities (Zhang et al., 2014; de Munck et al., 2017; Beltrachini, 2019a).

Some methods have been proposed to improve the behavior of the FEM in singularity cases, e.g., the subtraction method (Awada et al., 1997; Zhang et al., 2014; Beltrachini, 2019a; Darbas and Lohrengel, 2019) and the direct methods (Yan et al., 1991; Buchner et al., 1997; Hallez et al., 2007; Zhang et al., 2014). The subtraction method has a reasonable mathematical basis for point current dipole models. However, it is computationally relatively expensive and sensitive to conductivity jumps if the source is near them (Awada et al., 1997; Wolters et al., 2007; Lew et al., 2009; Beltrachini, 2019a,b). On the other hand, The direct FEM approaches such as St. Venant (Buchner et al., 1997) and partial integration (Yan et al., 1991) are easy to implement and have a much lower computational complexity, so they are very fast (Lew et al., 2009; Vorwerk et al., 2019b). However, the potential distribution strongly depends on the shape of the element at the source location (Awada et al., 1997; Medani et al., 2015). Among the direct approaches, the St. Venant approach was shown to have the most accurate results for the sources of not very high eccentricity (Vorwerk et al., 2019b). On the other hand the partial integration approach was shown to have higher stability even at the sources of high eccentricity (Medani et al., 2015).

On the other hand, the BEM is used for calculating the potentials of surface elements on the interface between compartments generated by a current source in piece-wise homogenous volume. The BEM can construct realistic geometry of piece-wise homogeneous isotropic compartments and solve the EEG forward problem accurately (de Munck et al., 2017). Also, it has numerical stability and effectiveness compared with differential equation-based techniques (Rahmouni et al., 2017; Monin et al., 2020). Unfortunately, the BEM formulations can be complicated to model complex geometry such as inhomogeneity, anisotropicity and surfaces with holes (Adde et al., 2003; de Munck et al., 2017; Rahmouni et al., 2017). Also, the BEM produces dense matrices that cause high computational cost compared with FEM (Adde et al., 2003).

In order to benefit from the advantages of both BEM and FEM, some coupled boundary element (BE)–finite element (FE) methods have been proposed in electromagnetic and biomedical problems (Bradley et al., 2001; Sikora et al., 2004; Olivi et al., 2010; Srinivasan et al., 2010; Ghaderi Daneshmand and Jafari, 2013). In Bradley et al. (2001), a new high-order cubic Hermite coupled FE/BE method has been proposed only for an isotropic three-layer spherical and realistic head model, and generalized Laplace’s equation had been solved. Also, a hybrid BE–FE method has been applied to the 2D forward problem of electrical impedance tomography (EIT) (Sikora et al., 2004) and has been used for modeling Diffusion equations in 3D multi-modality optical imaging (Srinivasan et al., 2010). A 3D coupling formulation was presented in Olivi et al. (2010) for solving the EEG forward problem iteratively. A domain decomposition (DD) framework was used to split the global system into several subsystems with smaller computational domains. Then, for each subsystem, one of the methods (BEM or FEM) was used. Several iterations were needed to solve the forward problem on the global system, and a relaxation parameter at each interface was compulsory to ensure convergence. The relaxation parameters were set manually, and an inappropriate value of these parameters would make the scheme diverge. Furthermore, three-layer concentric sphere models considering both the isotropic and anisotropic conductivity of the skull layer with dipoles of six locations and three orientations were modeled. No realistic head model was investigated. The coupling process was very time-consuming because the BEM and FEM ran iteratively until the relative residuals reached below a properly set value (6 × 10−5).

In Ghaderi Daneshmand and Jafari (2013), a hybrid BE–FE method, which directly combines the two BE and FE methods, has been proposed to solve the forward problem of EIT for a 3D cylindrical model of the human thorax. It should be noted that the EEG forward problem is completely different from the EIT forward problem regarding equations and boundary conditions. Thus, we must reformulate equations and extend them to be suitable for applying to the EEG forward problem. The advantage of using such a hybrid BE-FE method for solving the EEG forward problem is that the isotropic and homogeneous subregions containing the current dipoles can be modeled by the BEM and the other subregions (the inhomogeneous or anisotropic subregions or those without current dipoles) can be modeled by the FEM. Also, this method solves the global system in one step without any iteration. Consequently, it is expected that the application of the hybrid BE–FE method increases the accuracy of the EEG forward solution and consequently helps to more accurate localization of brain sources.

In this paper, BEM, partial integration FEM (PI-FEM), and hybrid BE–FE method, are employed to solve the EEG forward problem. To validate the hybrid BE-FE method in solving the EEG forward problem of isotropic multi-compartment media, we will use an isotropic piece-wise homogeneous three-layer spherical head model (brain, skull and scalp), which has an analytical forward solution, and the results will be compared with those of BEM and PI-FEM. To validate the hybrid BE-FE method in solving the EEG forward problem of anisotropic multi-compartment media, we will use an anisotropic three-layer spherical head model (brain, skull and scalp) in which the conductivity of the skull will be considered anisotropic and compare the results with those of PI-FEM. Since the cerebrospinal fluid (CSF) layer highly affects the scalp potentials (Ramon et al., 2006; Vorwerk et al., 2014), we will also investigate the performance of the hybrid BE-FE method compared with PI-FEM when considering the fourth layer for CSF and the anisotropic conductivity of the skull.

Because the conductivity uncertainties of head layers (especially skull and brain) have a significant influence on the EEG forward solution (Vorwerk et al., 2019a), we will repeat the simulation of each spherical head model 50 times with different realizations of conductivity of layers followed by statistical analysis to demonstrate the effect of conductivity uncertainties on the EEG forward solution. Finally, the hybrid BE-FE method and PI-FEM will be compared on a four-layer realistic head model in which the conductivity of the skull will be anisotropic.

This paper is organized as follows: In Section 2, the mathematical model for the EEG forward problem and its numerical solutions using BEM, PI-FEM, and hybrid BE–FE method was formulated. In Section 3, the performance criteria for validation were described. In Section 4, the results of simulated spherical and realistic head models were reported. In Section 5, the results were discussed. Finally, in Section 6, the paper was concluded, and some future works was proposed.

2 Mathematical model 2.1 EEG forward problem

The EEG forward problem entails calculating the electric potential ? on the scalp surface ? (see Figure 1A). These potentials are generated by current dipoles within the head volume R. Therefore, since the relevant frequencies of the EEG spectrum are below 100 Hz, the quasi-static approximation of Maxwell’s equations is used to estimate the electric potentials over the scalp with homogeneous Neumann boundary conditions at each time sample (t) as follows (Hämäläinen et al., 1993):

∇.σ∇φt=∇.JPtinsideRfor each time sampletσ∂φ/∂n=0onS    (1)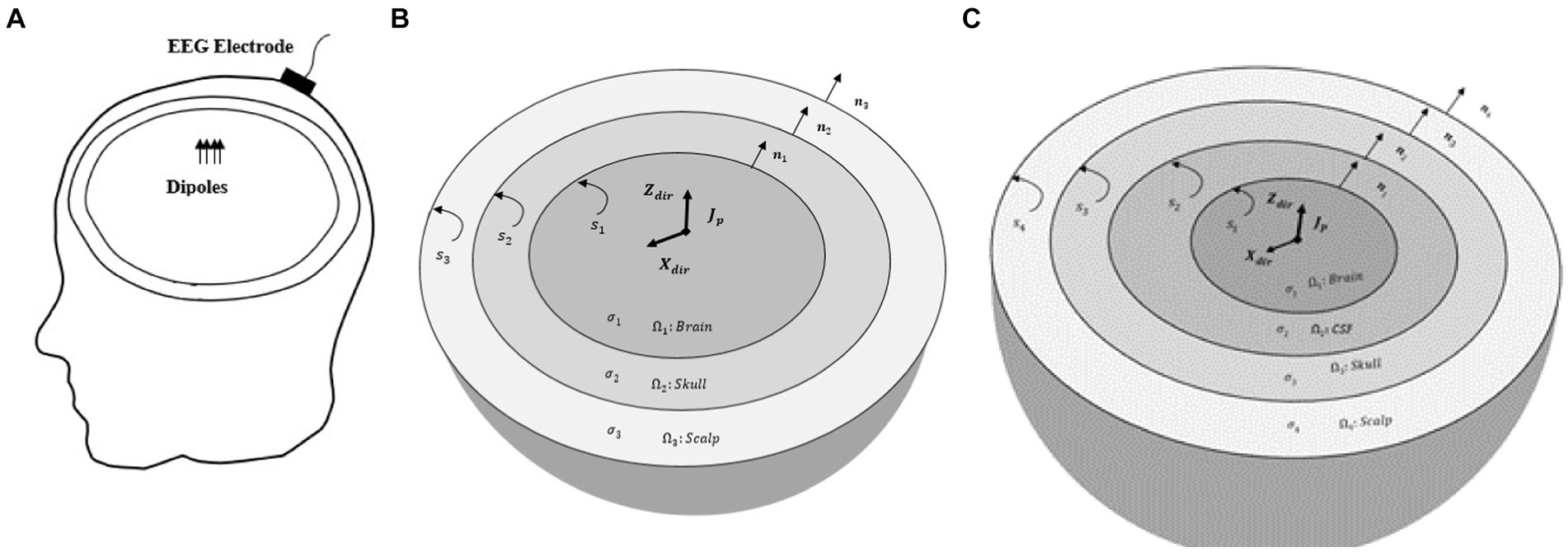

Figure 1. (A) EEG forward model. Electric potentials recorded by EEG electrodes are generated by dipoles within the head volume. A sample EEG electrode placed on the scalp is only shown. (B) The piece-wise homogenous three-layer spherical head model (brain, skull, and scalp). S1, S2, and S3 are the interfaces between brain-skull, skull-scalp, and scalp-air, respectively. Also, n1, n2 and n3 are the outward unit normal vectors of brain, skull and scalp layers. (C) The piece-wise homogenous four-layer spherical head model (brain, CSF, skull, and scalp). The conductivity of the skull can be isotropic or anisotropic. S1, S2, S3, and S4 are the interfaces between brain-CSF, CSF-skull, skull-scalp, and scalp-air, respectively. n1, n2, n3, and n4 are the outward unit normal vectors of brain, CSF, skull and scalp layers, respectively.

where ?: ℝ3 → ℝ3 denotes conductivity tensor of tissue conductivity in R and ?? denotes the primary current density of the brain source. Also, n is the outward unit normal vector at the surface S (Hämäläinen et al., 1993; de Munck et al., 2017). In this manuscript, vector quantities are denoted by bold characters.

The primary current density ?? is commonly modeled as two delta functions at the current source position

?2 (?2, ?2, ?2) and the current sink position ?? (?1, ?1, ?1) with the current source density I as follows (Hallez et al., 2007):

∇⋅JPx=Iδr–r2−δr–r1    (2) 2.2 Boundary element method

In the Boundary element method (BEM), the reciprocal relation is applied to derive a boundary integral equation for the boundary value problem Equation (1) as given by Ang (2007).

λξηζφξηζ− ∭RΦ3Dxyzξηζgxyzdxdydz=∬S[φxyz∂∂nΦ3Dxyzξηζ−Φ3Dxyzξηζ∂∂nφxyz]dsxyz    (3)

where ? (?, ?, ?) = 1/?∇. ?P , λ(?, ?, ?) is a characteristic function of the domain R, ? is the conductivity of domain that must be constant and isotropic. The function ?3D (?, ?, ?; ?, ?, ?) is the fundamental solution of the three dimensional Laplace’s equation and is given by Equation (4) Ang (2007).

Φ3Dxyzξηζ=−14πx−ξ2+y−η2+z−ζ2    (4)

Consider the surface of a region to be discretized to N triangular elements. The potential ϕ (?, ?, ?) and its normal derivative ?/?? [?(?, ?, ?)] are approximated as constant values over each element as Equation (5):

φ≃φ¯kand∂φ∂n≃p¯kforxyz∈Skk=1,2,…,N    (5)

where ?̅(?)and ?̅(?) are the average values of ? and ?ϕ/?? on the centroid point of the kth surface element, ?(?).

Using these approximations, Equation (3) is simplified as

λξηζφξηζ− ∭RΦ3Dxyzξηζgxyzdxdydz=∑k=1Nφ¯kD2kξηζ−p¯kD1kξηζ    (6)

where

D1kξηζ= ∬SkΦ3DxyzξηζdsxyzD2kξηζ= ∬Sk∂∂nΦ3Dxyzξηζdsxyz    (7)

Let (?, ?, ?) in Equation (6) be given consecutively by the centroid point of S(1), S(2), …, S(N). D1(k) and D2(k) were introduced in Equation (7). Consequently, Equation (6) can be rewritten as Ang (2007).

12φ¯m− ∭RΦ3Dxyzξηζgxyzdxdydz=∑k=1Nφ¯kD2kx¯my¯mz¯m−p¯kD1kx¯my¯mz¯mform=1,2,…,N    (8)

where (?̅(?), ?̅(?), ?̅(?)) is the centroid point of the element ?(?). On the typical element S(?), either ?̅(?) or ?̅(?) is known. Thus Equation (8) constitutes a system of N linear algebraic equations including N unknowns for a one-layer homogenous region as given by Ang (2007).

where ??? is the column vector (column matrix) including both ?̅ and ?̅ for each element, ??? is the coefficient matrix and ??? is the column vector containing values of boundary condition and the current dipoles information. Equation (9) describes the matrix form of the BEM for just one homogenous subregion.

In order to implement BEM for multi-layer piece-wise homogeneous media, we used the same approach as that of Ghaderi Daneshmand and Jafari (2013). Hereby, we describe that method for a three-layer spherical head model with nested regions of constant conductivity (see Figure 1B). First, all interfaces are discretized to N triangles, and then the first subregion (brain) is represented by Equation (1). Other subregions (skull and scalp) are represented by the Laplace equation. The first and second boundaries of each subregion are assumed to be Dirichlet and Neumann conditions, respectively. Considering the air/scalp interface, the boundary condition of the second boundary of the scalp is of Neumann type. The system of linear algebraic equations for each subregion is obtained as Equation (10) (Ang, 2007):

ABEjXBEj=BBEjj=1,2,3    (10)

where ???j is the column vector including both ?̅ and ?̅ for each element at the jth subregion. Assembling the

equations corresponding to all subregions, the same algebraic equation as Equation (9) is derived. Then, continuity conditions at the interface between two adjacent subregions should be applied to the resulting equation. The continuity condition for the electric potential and continuity condition for the normal component of the current density at the interface surface ???−?? are given as Equation (11) (Ang, 2007):

φBEi=φBEjσBEi∂φBEi∂ni=σBEj∂φBEj∂nj    (11)

where (????, ????) and (????, ????) are the (electric potential, conductivity) of each element on the interface between two adjacent subregions Ω??? and Ω???, respectively. After the continuity condition for the electric potential and the normal component of the current density, the electric potential and its normal derivation of surface elements are computed by using Gaussian elimination method.

2.3 Finite element method using partial integration approach (PI FEM)

In the FEM, the functional F(?) derived from the Rayleigh-Ritz method, a variational method, is minimized to solve the boundary value problems. Equation (1) can be written in Cartesian coordinates with homogeneous Neumann boundary conditions Equation (12) (Jin, 2014).

∂∂xσx∂φ∂x+∂∂xσy∂φ∂y+∂∂zσz∂φ∂z=∇·JPσ∂φ∂n=0onS    (12)

Consequently, the functional is defined as Jin (2014):

Fφ=12∫Rσx∂φ∂x2+σy∂φ∂y2+σz∂φ∂z2dR−∫R∇·JPφdR    (13)

where ??, ?? and ?? are, respectively, the conductivity along x, y and z axes that are constant and equal to each other in isotropic media but unequal to each other in anisotropic media.

The first step of the FEM is the discretization of the regions into a number of tetrahedral elements. The unknown potential ?? at any point within each tetrahedral element can be approximated as Equation (14) Jin (2014):

φexyz=∑j=14Njexyzφje    (14)

where the interpolation functions ?j?(?, ?, ?) are given by Equation (15).

Njexyz=16Veaje+bjex+cjey+djez    (15)

where ?j ?, ?j ?, ?j ? and ?j ? are constants and are determined from the coordinates of the nodes of elements (Jin, 2014). By minimizing the functional ?(?) in Equation (13) for each element and assembling all elements in the whole volume, and using the partial integration (PI) approach to model the current dipoles (Yan et al., 1991; Schimpf et al., 2002), the final set of equations can be written as follows (Jin, 2014).

where ??? is the coefficient (stiffness) matrix, which is a function of nodal coordinates and conductivity of each element. ??? is the column vector of the unknown electric potential of the nodes and ??? is the source column vector contributed by the dipoles that has non-zero entries for the set of nodes of the elements that contain the dipoles. After the Neumann boundary condition, given in Equation (1) is applied to Equation (16), the electric potential is computed by using quasi-minimal residual method. It is noteworthy that in FEM, another approach called Galerkin which is the weighted residuals method can be used (Jin, 2014; Munafò et al., 2023).

2.4 Hybrid BE–FE method

The hybrid BE–FE formulation consists of both FE and BE formulations. It is implemented by combining Equation (9) with Equation (16) and applying boundary conditions in each interface. First, the BEM is used to represent the Poisson Equation (1) at the brain subregion (BE region) considering the Dirichlet boundary condition. Then FEM is used to represent the Laplace equation (∇. (?∇?) = 0) at other subregions (FE regions) considering Neumann condition at skull/brain and air/scalp interfaces for the three-layer spherical head model, and CSF/brain and air/scalp interfaces for the four-layer spherical head model to derive Equation (16). The values of boundary conditions on each interface are unknown. Assembling Equations (9) and (16) gives.

KFE00ABEφBEXBE=BFEBBE    (17)

To solve Equation (17), the value of boundary condition at the BE-FE interface must be applied but it is unknown. To apply boundary condition on a BE-FE interface S??−??, the potential on S??−?? computed from both BE region and FE region must be the same. Since the potential on a surface BE element is constant, but in a FE element is linear, in order to equalize those potentials on the BE-FE interface, one may take the average of three FE nodal potentials and obtain the following approximation for the BE surface element potential as Ghaderi Daneshmand and Jafari (2013).

φBE=φFE1+φFE2+φFE33    (18)

where ???1, ???2, and ???3 are FE nodal potentials at each element in S??−??. The continuity condition for the normal component of the current density at S??−?? yields Equation (19) (Ghaderi Daneshmand and Jafari, 2013).

σFE∂φFE∂nFE=−σBE∂φBE∂nBE    (19)

Applying Equations (18, 19) to (17), the matrices ???, ???, ???, and ???, are modified as ?̃??, ?̃??, ?̃??, and ?̃??, respectively; and the resulting equation is obtained as.

K˜FEMFEMBEA˜BEφFEXBE=B˜FEB˜BE    (20)

where ??? and ??? are sparse matrices constructed as a result of applying Equations (18, 19), respectively. Using Gaussian elimination method, Equation (20) is solved for ??? and ???.

To use the hybrid BE-FE method, two important points should be considered:

First, when an anisotropic piece-wise homogenous multi-layer medium is modeled, the layer(s) containing dipoles must be modeled with the BEM, and the layers with anisotropic conductivity must be modeled with the FEM. Other layers can be modeled with each of FEM or BEM depending on our goals, such as less time and memory consumption, and computational complexity. So in this paper, we used the FEM for other layers. Also, we will show the performance of the hybrid BE-FE method when only one layer, including current dipoles is modeled with the BEM, and we compare this performance with the performance of FEM.

Second, we used linear elements in the FEM. Thus, to couple BEM and FEM elements, we need constant triangular elements or continuous linear triangular elements in BE domain to use Equations (18, 19). We prefer to use constant elements in the BEM because solving forward problem with constant elements is more accurate than continuous linear elements (Ang, 2007).

It should be noted though the discontinuous linear element is more accurate than constant and continuous linear elements, it cannot be used to couple with the FEM in our method and because in our method, we need the constant potential in the surface BE elements or the vertex’s potentials of BE elements to use in Equation (18).

2.5 Tetrahedral mesh generation

To implement the FEM and BEM, the entire region is first discretized into tetrahedral volume elements for the FEM, and then the required surface triangular meshes in the BEM are prepared from the data of tetrahedral elements of the entire region. For mesh extraction, we use ISO2MESH (Fang and Boas, 2009) that provides us with accurate mesh volume and surface elements.

In the hybrid BE–FE method, the BE regions and the FE regions are discretized using a triangular surface mesh and a tetrahedral volume mesh, respectively. In order that the BE and FE regions in the hybrid method have the same boundary surface elements, the entire volume domain is first discretized by irregular tetrahedral volume elements, and then irregular triangular surface elements for the BE regions are extracted from the data of the tetrahedral elements. It is noteworthy that the FEM uses the entire tetrahedral volume elements.

In the realistic head model, we can leverage on FieldTrip software to obtain an automatic segmentation of the brain, CSF, skull, and scalp (Oostenveld et al., 2011). By using FieldTrip, the surface boundaries of these four structures are extracted. Then, based on the boundaries, a finite element model can be constructed by ISO2MESH (Fang and Boas, 2009).

3 Validation method 3.1 Validation platform

To validate the precision of the proposed hybrid BE-FE method, it was essential to employ a model with a known analytical solution within the domain of bioelectromagnetism, serving as a reliable reference or “ground truth.”

To fulfill this requirement, we opted for spherical models due to their similarity to real-world scenarios and the availability of analytical solutions. So, the proposed hybrid BE-FE method is validated and compared with the FEM and BEM, with simulating piece-wise homogeneous three- and four-layer spherical head models.

We will first simulate an isotropic, piece-wise homogeneous three-layer spherical head model with radial and tangential dipoles of six different eccentricities. Then, we will repeat the same simulation but with an anisotropic layer (skull) to show the performance of FEM and the proposed hybrid BE-FE method when the skull is modeled as a layer of homogenous and anisotropic profile. Afterward, we will add a fourth layer for CSF to the previous anisotropic model. This layer has an important role in distributing the currents in the head model and scalp potentials (Ramon et al., 2006; Vorwerk et al., 2014). Next, we will repeat the same procedure to assess the performance of the hybrid BE-FE method on this anisotropic and piece-wise homogeneous four-layer medium.

To extend the applicability of our findings to authentic scenarios, we will conduct additional investigations using a real head model. Consequently, we will compare the proposed hybrid BE-FE method with the FEM on an anisotropic piece-wise homogeneous four-layer realistic head model. Based on this comprehensive approach, encompassing both analytical and real-world evaluations, will contribute to a robust validation of the efficacy and reliability of our proposed numerical method.

To assess the precision of our proposed numerical method in addressing the forward problem and its associated influencing factors, it is essential to hold all influencing factors constant while varying only one selection variable. These factors are the precision of head model segmentation, mesh quality, conductivity variations in different head layers, and the positioning and orientation of dipoles (Miinalainen et al., 2019; Vorwerk et al., 2019a; Nielsen et al., 2022). Therefore, we will evaluate hybrid BE-FE method according to conductivity uncertainties of head layers for each of the above spherical head models and dipoles’ positions and orientations. We will simulate 50 realizations using randomly chosen conductivity values from realistic intervals. This allows us to gain a statistical overview of the precision of solving EEG forward problem with regard to the electromagnetic properties of head layers.

In each of the above models, unit radial (along z-axis) and tangential (along x-axis) dipoles of six different eccentricities will be considered. For each dipole, the source eccentricity is defined as the percentage of the Euclidian distance between the dipole location and the sphere center divided by the radius of the innermost shell (Wagner et al., 2016). In our implementations, the most eccentric dipole has an eccentricity of 98%.

In this paper, for spherical head models, we use the analytical solution given in Zhi (1995) that calculates the electric potential on the outmost surface (scalp) of isotropic/anisotropic multi-layer spherical head model generated by a dipole inside the innermost layer (brain). For the realistic head model, we use a refined model of the FEM to obtain a reference FE solution because an analytical solution is unavailable for real models.

It is noteworthy that in all of our simulations, in order to have fair comparisons between the accuracy of the FEM, BEM and hybrid BE-FE method, we choose the mesh resolution that their computation times are nearly the same.

3.2 Error criteria

The error between the numerical solution and analytical solution can be obtained by Relative Difference Measure (RDM) and the Magnitude ratio (MAG) (Mejis et al., 1989; de Munck et al., 2017). These measures are, respectively, defined as Equations (21) and (22):

RDM=|φAnaφAna−φNumφNum|    (21) MAG=|φNumφAna|    (22)

where ???? and ???? are analytical and numerical solutions, respectively and | | denotes the square root of Euclidean distance. In this paper, ???? is calculated by using the analytical solution given in Zhi (1995) for spherical head models and the reference FE solution obtained from the refined model of the FEM for the realistic head model.

4 Simulation results

In this paper, the performance of the hybrid BE-FE method to solve the EEG forward problem will be assessed using both spherical and realistic head models. In the spherical models, the solution will be evaluated on all outer boundary (scalp) nodes instead of the small number of them so that the results are nearly independent of the choice of electrode positions (Vorwerk et al., 2017). On the other hand, for the realistic head model, the results will be assessed on 90 positions of the scalp surface. It is noteworthy that other influential factors on solving forward problem were considered completely the same.

4.1 Example I: isotropic piece-wise homogenous three-layer spherical head model

To compare the performance of hybrid BE-FE method with the BEM and PI-FEM, a numerical validation will be performed using a three-compartment (brain, skull and scalp) spherical head model as shown in Figure 1B with parameters indicated in Table 1 (Malmivuo and Plonsey, 2002; Vorwerk et al., 2019a). The optimized anisotropy ratio in Table 1 is defined as the ratio of radial conductivity (??) to tangential conductivity (??) of the skull (Dannhauer et al., 2011). In this simulation, the PI-FEM mesh has 6,808 nodes and 34,428 tetrahedral volume elements, the BEM mesh has 3,092 triangular surface elements, and the hybrid BE-FE mesh has 2,578 nodes, 10,688 tetrahedral volume elements and 1894 triangular surface elements.

Figures 2, 3 show boxplots of RDM and MAG of PI-FEM, BEM, and hybrid BE-FE method for isotropic and piece-wise homogeneous three-layer spherical head models versus different eccentricities of the dipole for radial and tangential dipoles, respectively. For each model, 50 realizations were simulated by randomly chosen conductivities from intervals shown in Table 1. Also, the mean and standard deviation of RDM and MAG and p-values of Wilcoxon signed-rank tests are reported in Table 2. It should be noted that some datasets did not pass the Gaussian test (p-value < 0.05). For this reason, we used Wilcoxon signed-rank test to calculate p-values. The significant differences are shown as gray in Table 2.

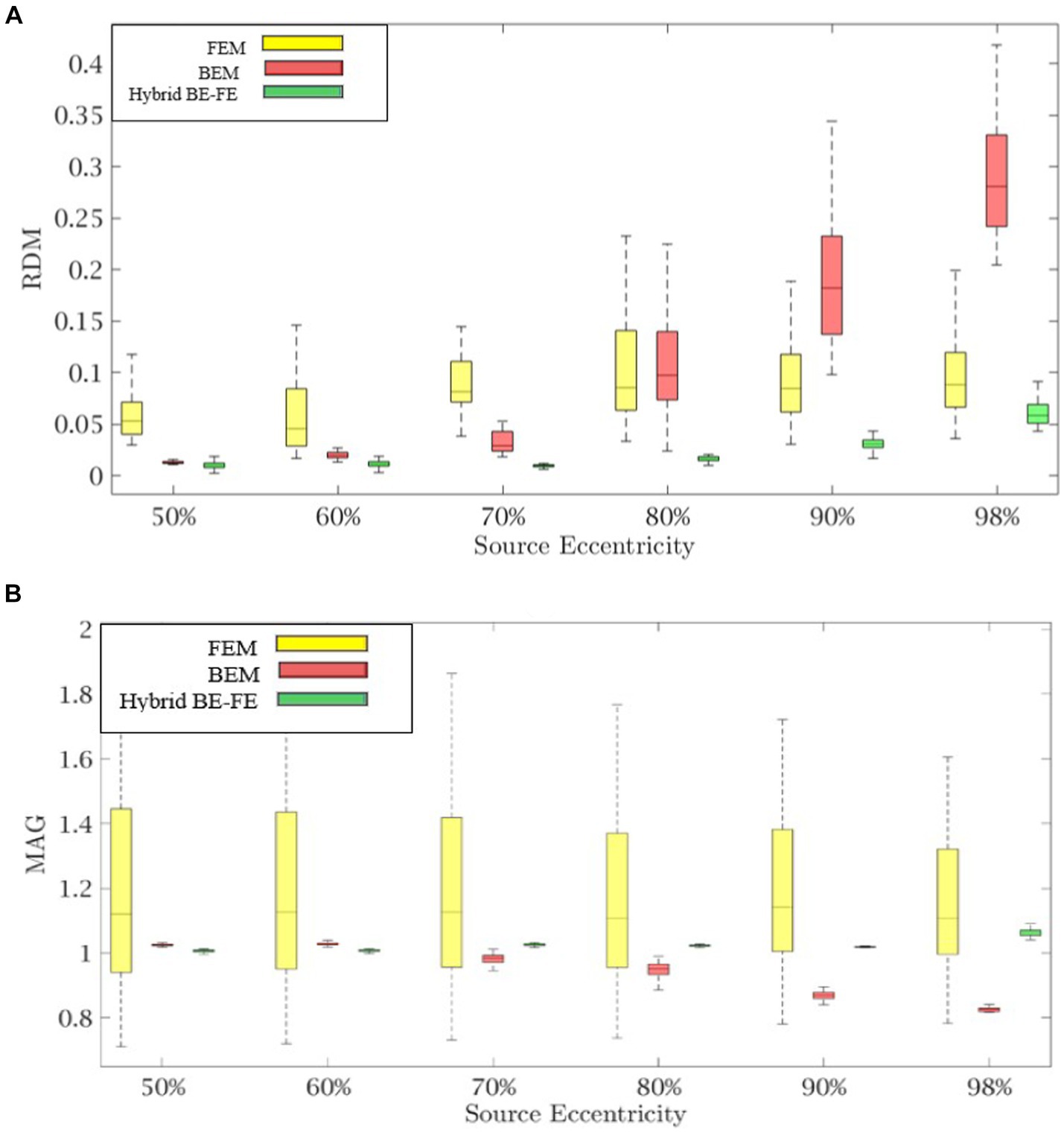
Figure 2. Example I: isotropic piece-wise homogenous three-layer spherical head model for radial dipole orientation (z-axis), (A) RDM and (B) MAG boxplots of PI-FEM, BEM, and hybrid BE-FE method at six different source eccentricities.

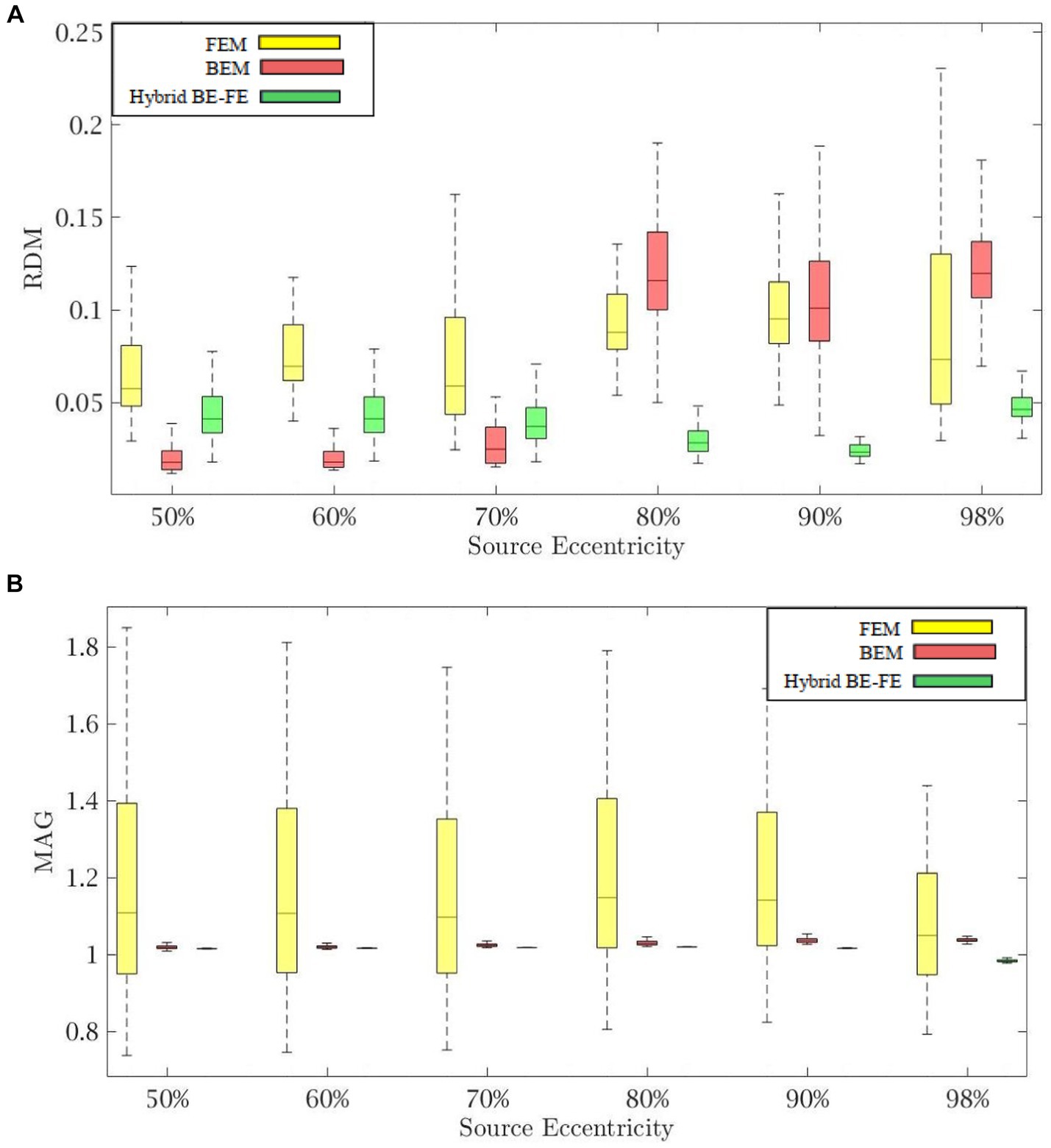
Figure 3. Example I: isotropic piece-wise homogenous three-layer spherical head model for tangential dipole orientations (x-axis), (A) RDM and (B) MAG boxplots of PI-FEM, BEM, and hybrid BE-FE method at six different source eccentricities.

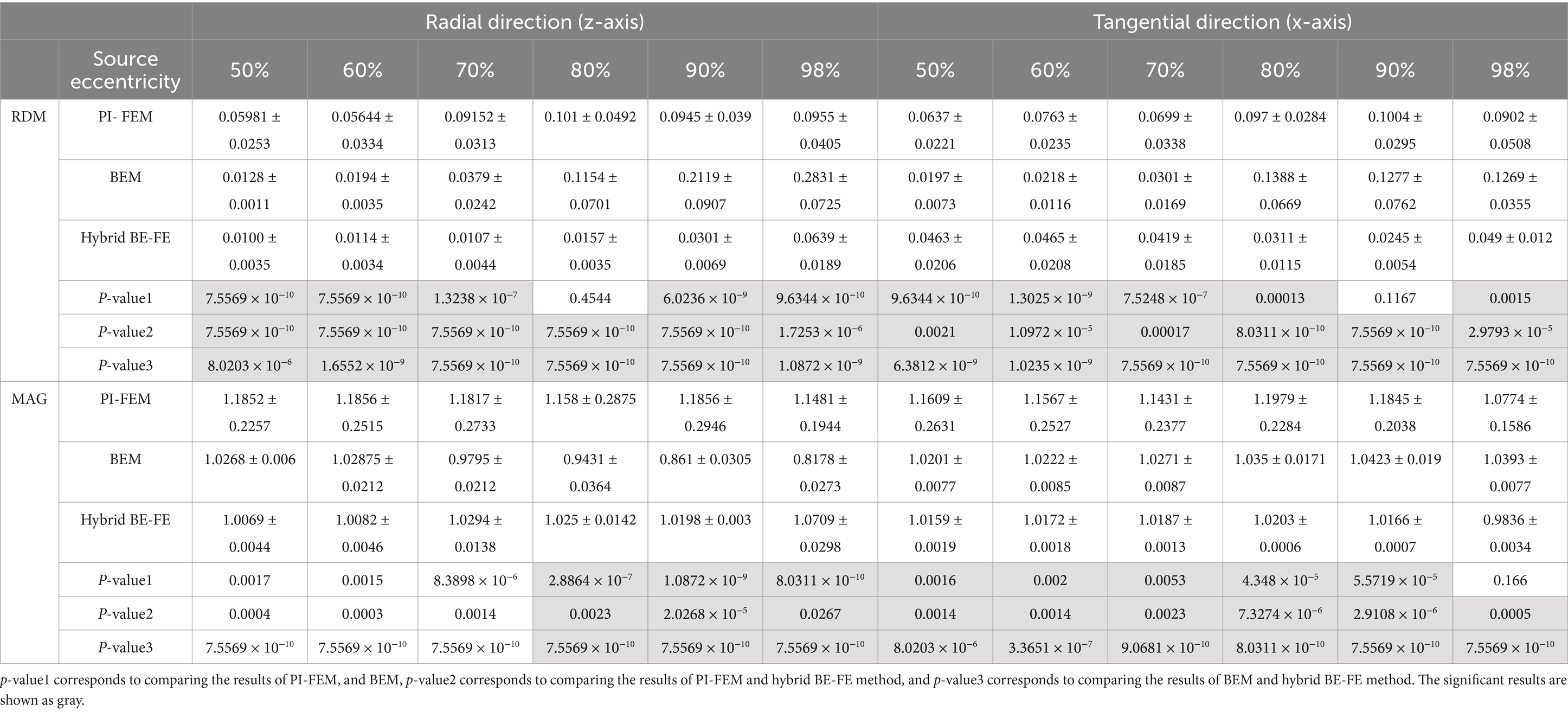
Table 2. Example I: isotropic piece-wise homogeneous three-layer spherical head model, mean ± std. and p-value of Wilcoxon signed-rank test of 50 realizations of RDM and MAG obtained from PI-FEM, BEM and hybrid BE-FE method for dipoles of six different source eccentricities and both radial and tangential directions.

Comparing the PI-FEM, BEM, and hybrid BE-FE method with regard to the RDM for isotropic piece-wise homogeneous three-layer spherical head model (Figure 1A) shows that the hybrid BE-FE method significantly outperforms the PI-FEM for dipoles of both radial (Figure 2A) and tangential (Figure 3A) directions and all six eccentricities. In the radial direction, the hybrid BE–FE has a maximum RDM of 0.0639 ± 0.0189 at 98% source eccentricity, and the PI-FEM has its maximum RDM of 0.0955 ± 0.0405 at the same source eccentricity (Figure 2A). Also, the PI-FEM leads to a larger RDM variance than the hybrid BE-FE method. In the tangential direction, the maximum RDM obtained from the hybrid BE-FE method is 0.049 ± 0.012 at 98% source eccentricity, while the FEM is higher RDM (0.0902 ± 0.0508) at these eccentricities. On the other hand, the maximum RDM obtained from the PI-FEM is 0.1004 ± 0.0295 at 90% source eccentricity (Figure 2A).

For dipoles of radial directions, the hybrid BE-FE method significantly outperforms the BEM. The hybrid BE– FE method has a maximum RDM of 0.0639 ± 0.0189 at 98% source eccentricity and the BEM has its maximum RDM of 0.2831