Antibiotic responses in bacteria are remarkably dynamic and heterogeneous. Microbes typically carry regulated mechanisms of antibiotic resistance, which are repressed when the drug is absent to avoid the costs associated with expression of resistance genes [1, 2]. Therefore, when challenged by antibiotics, the cell has only a small window of time to activate its defenses before gene expression is halted by the drug action. Since expression of resistance genes is subjected to the strong stochasticity inherent to bacterial physiology, induction of the response is not always successful [3–5]. Sudden exposures to antibiotics have been shown to result in phenotypic heterogeneity, diversity of response outcomes in single cells and complex growth patterns at the population level [6–12]. To understand how microbial populations survive antibiotic treatments, we need models of antibiotic responses accounting for the dynamic and heterogeneous nature of antibiotic resistance.

Following antibiotic exposure, expression of resistance genes is controlled not only directly by regulatory mechanisms, but also indirectly by global effects of the drug on cell growth and gene expression, with a growing body of literature linking metabolism to the ability of bacteria to resist antibiotic treatments [13–15]. Accumulation of resistance proteins in the cell interior depends on the resistance gene's expression rate and on the dilution of cell components due to cell growth, both of which are affected by the cell's metabolic environment. The presence of antibiotics itself alters the cell's growth dynamics and allocation of metabolic resources [16], which in turn affect expression and dilution of resistance, and consequently survival upon drug exposure. During drug responses, many antibiotics hamper the induction of resistance genes, which leads to further drug accumulation and decreased expression [17]. These metabolism-mediated feedback mechanisms affect the course of antibiotic responses and can potentially amplify stochastic variations resulting in the coexistence of live and arrested cells [18]. Stochastic generation of phenotypic diversity has also been studied in other systems, such as persistence, where a few cells from an isogenic population resist antibiotic exposures by growing slowly [19, 20], or in heat stress responses in yeast [21].

Due to their small size, cellular components in bacteria are often present in small numbers and are subject to stochastic fluctuations. In particular, the transcription factors that regulate gene expression are often present on the order of tens of molecules per cell. Therefore, transcriptional regulation greatly increases stochasticity in gene expression, leading to strong variability in expression levels even among genetically identical cells [22, 23]. When this variability is high, it can be harnessed as a resistance strategy under stressful conditions [4, 24–27]. Bacterial colonies often harbor a subpopulation of cells with high levels of resistance proteins prior to drug exposure, increasing the chances of colony survival (heteroresistance) [28, 29]. However, even in the absence of strong pre-existing heterogeneity, subtle variations in the expression of resistance genes can be amplified during antibiotic responses by regulatory mechanisms controlling gene expression [30], diverging the course of responses among single cells, and ultimately leading to phenotypic heterogeneity at the population level. Therefore, isogenic populations growing under homogeneous environmental conditions still show remarkable diversity of outcomes at the single-cell level during antibiotic responses [24, 31].

Here, we develop mathematical models of the dynamics of an antibiotic response, incorporating drug effects on cell growth and gene expression, to explain the emergence of heterogeneity during drug exposures. We start with a deterministic model that reproduces the progression of drug accumulation, expression of resistance and cell growth during a drug response. Then we develop a stochastic model to show how noisy dynamics can lead to phenotypic heterogeneity. We base our models on the classical E. coli tetracycline resistance tet operon, which displays many general characteristics of regulated antibiotic responses [26, 32, 33]. The tet resistance mechanism is tightly regulated, controls a resistance gene that poses a significant cost for the cell, and is not directly regulated by other cellular processes [6, 34, 35]. Cells carrying the native tet operon were shown to coexist in growing and non-growing states upon exposure to a large dose of tetracycline [6]. The tet operon consists of two genes, an efflux pump TetA and its repressor TetR. In the absence of tetracycline, TetR represses both TetA expression and its own [36]. TetR has a strong affinity for tetracycline, binding the drug as it enters the cell, which causes a conformational change resulting in loss of affinity for DNA and release of expression of both TetA and TetR. Efflux pump TetA is then rapidly produced, exporting tetracycline out of the cell. As the intracellular tetracycline concentration decreases, TetR resumes repression, avoiding a toxic overexpression of TetA [37]. Since the tet mechanism directly senses the intracellular presence of the drug and elicits a fast and strong response, it is an ideal system to study antibiotic response dynamics and heterogeneity.

We describe the response dynamics of a widespread mechanism of regulated antibiotic response, which is broadly applicable to other responses where the cell needs to react quickly to rapidly changing environments [6, 13, 38], bringing the system out of equilibrium. Since the dynamics described in our model are not particular to antibiotic resistance mechanisms, many insights from this formulation can also be generalized to other transcriptionally repressed cellular responses that both sense and negatively act upon a chemical signal.

To capture the dynamics of cell responses, we developed a mathematical model based on the main biochemical interactions involved in the E. coli tetracycline response (figure 1(a)). We integrate drug diffusion and accumulation into the cell, transcriptional regulation, and expression of resistance genes, as well as global effects of the drug on cell growth and gene expression. Tetracycline is a ribosome inhibitor [39], which reduces cell growth [40] and causes the cell to upregulate ribosome production in response [41]. Altered ribosome levels then result in changes in the partition of the proteome [41, 42], affecting expression of non-ribosomal genes including antibiotic resistance (described in detail below). Since in our model the cell growth rate is variable, a cell dies when the drug action causes ribosome function to cease, and the growth rate becomes zero. This system is largely governed by two feedback mechanisms: a stabilizing negative feedback provided by transcriptional repression [43–47], and a positive feedback mediated by the metabolism (growth rate-dependent) that can lead to bistability [18, 48].

Figure 1. Drug concentration affects recovery from antibiotic exposures. (a) The tet resistance mechanism. Tetracycline (Tc) diffuses across the cell membrane, and binds repressor TetR, thereby releasing expression of TetA and TetR. TetA then exports the drug outside the cell. Tetracycline also binds ribosomes, inhibiting protein translation. Solid arrows represent protein synthesis, solid bi-directional arrows represent binding/unbinding, blunted arrows represent repression, dashed arrows represent import/export of tetracycline, and dotted arrows represent ribosome content promoting protein synthesis. (b) Schematic of the microfluidic device used for measuring growth and expression of resistance in single cells during drug exposures. The experimental data in this figure is reproduced from [6]. (c) Average tetracycline, TetA, and TetR levels over the course of a response, measured in 40 tetracycline-resistant single E. coli cells during a microfluidic experiment. (d) Tetracycline, TetA and TetR levels over the course of a response as predicted by our deterministic model. (e) Three examples of time courses of single cells, resulting in different cell fates. Red and green colors represent expression of TetA and TetR, respectively, measured with fluorescent reporters. (f) Cell growth in single cells following a sudden tetracycline exposure (thin lines). Yellow, red, and black lines correspond to recovered, moribund, and arrested cells, respectively. Thick lines represent average growth within each group. Moribund cells that grow slowly following drug exposure eventually either recover or become arrested. (g) Varying the dissociation constant for drug-ribosome binding, the model reproduces the responses seen in single cells. (h)–(j) Growth rate, TetA, and TetR levels over the course of a tetracycline response, calculated at different extracellular drug concentrations. Higher drug concentrations lead to larger decreases in growth rate, eventually leading to arrest. (k) Recovery times increase with extracellular drug levels, approaching a vertical asymptote at a threshold drug concentration . (l) Growth rate at the end of the tetracycline response for different extracellular drug concentrations. The final growth rate drops sharply around the threshold drug concentration .

Download figure:

The model consists of a system of three differential equations that track changes in repressor TetR (), efflux pump TetA (), and intracellular drug () concentrations:

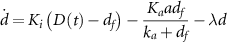
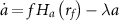
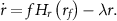
Intracellular drug concentration changes over time according to three processes: the influx of drug from the environment into the cell, the export of drug by the efflux pump TetA, and the dilution of intracellular components due to cell growth. Since tetracycline is not actively degraded in the cytoplasm [49–52] and TetA and TetR are stable proteins [53, 54], dilution due to cell growth is the main process driving down the concentration of these components [7] (except for efflux of tetracycline by TetA). Tetracycline enters the cell by diffusing through the cell membrane, with a rate proportional to the difference between the extracellular and intracellular drug concentrations ( and ) with a diffusion constant . Although diffusion through the hydrophobic membrane is relatively slow, with a half-equilibration time around 45 min [54, 55], intracellular tetracycline is already toxic for the cell at low concentrations in the nanomolar scale. Therefore, exposures to extracellular tetracycline in the micromolar scale, which tet-equipped E. coli can resist, still results in intracellular drug rapidly reaching toxic levels. Efflux pump TetA exports tetracycline out of the cell efficiently, following standard Michaelis–Menten kinetics described by where is the catalytic rate constant, and the Michaelis constant. In growing cells, the intracellular nanomolar concentrations of tetracycline do not significantly saturate TetA. As the cell grows, the drug is diluted in the cell interior, with the dilution rate equal to the growth rate . The cell growth rate is not fixed, and depends on drug action and metabolism, as detailed below.

In the cytoplasm, tetracycline strongly binds repressor TetR, which then undergoes a conformational change and loses capacity to bind its DNA binding site [6, 21]. Since biochemical binding and unbinding reactions happen at much faster timescales than the other relevant processes, we consider a chemical equilibrium between the unbound (free) forms of drug and TetR (, ) and the bound form , with an equilibrium constant . This equilibrium results in and , and the concentration of free TetR can be calculated by solving the resulting quadratic equation . While the bound form of TetR is inactive, the free form transcriptionally regulates expression of both TetA and TetR. TetA concentration changes over time according to its synthesis and its dilution due to cell growth . We model TetR regulation of TetA synthesis using a Hill function , which describes the equilibrium binding of free repressor TetR and its binding sites in the promoter region of TetA. is the fully induced expression rate, in the absence of TetR repression. Free repressor decreases TetA expression, with being the repressor level for half-maximal expression. The Hill coefficient is a measure of how sharply expression rates transition between high and low levels around the threshold , and is related to the cooperativity in TetR DNA binding. We use a Hill coefficient of to reflect TetR binding two different DNA binding sites as a dimer [36, 56] (SI). The factor modulates the expression of resistance proteins according to global effects of drug action on cell metabolism (cell growth) and is detailed below. TetR concentration is similarly determined by its synthesis and its dilution due to growth .

Even in the absence of drug, gene expression depends on the cell growth rate, which is set by the quality of the nutritional composition of the immediate environment. The cell grows according to the total output of translation, and therefore the growth rate is proportional to the ribosomal content of the cell. Faster growing cells then harbor larger ribosomal content, and consequently less non-ribosomal proteins. Additionally, since tetracycline is a ribosome inhibitor, it also causes the cell to upregulate ribosomal content, decreasing non-ribosomal content. A fraction of the proteome, thought to consist of housekeeping genes, rescales gene expression proportionally to the growth rate, balancing synthesis and dilution in order to maintain constant expression levels [41]. To accommodate for changes in ribosomal content, another variable fraction of the proteome adjusts its expression level in the opposite direction. In our model, we account for the effects of intracellular drug concentration and nutrient quality on gene expression and cell growth by incorporating a proteome partitioning framework developed by Scott et al [41]. According to this framework, all proteins in the cell fall within one of three categories: (1) Sector proteins whose concentrations are not affected by changes in ribosomal content, caused by changes in cell growth or translational inhibition by drug action (e.g. housekeeping genes), (2) Sector of ribosome-affiliated proteins, whose concentration increases with the growth rate or translational inhibition, and (3) Sector of all other proteins, whose concentration decreases with growth rate or translational inhibition to compensate for the increase in ribosomal proteins.

As the fraction of the cell's proteome that consists of proteins not affected by translational inhibition does not change, the allocation of resources towards ribosome-affiliated proteins and all others adds to a fixed portion of the proteome, with the two sectors varying according to the cell's translational () and nutritional () capacities. relates to ribosomal function, measured by the global rate of translation elongation, and relates to nutrient quality, or the capacity of the culture medium to support growth. Here, we refer to the base value of the cell's translational capacity in drug-free medium as , which has a universal value of 4.5 h−1 for E. coli [41] (henceforth, we use subscript or superscript 0 to indicate quantities under full-growth drug-free conditions). The translational capacity is reduced by the presence of intracellular drug, which binds and inactivates ribosomes, and can thus be modeled by , where is the dissociation constant for drug-ribosome binding. Lower values correspond to stronger inhibition, and vice versa. The nutritional capacity reflects the nutrient quality of the medium, where media with higher allow faster growth rates. Here, we focus our analysis on situations where nutrient quality does not change, such as in exponential growth in liquid cultures or stable growth in microfluidic devices, where can be determined as a fixed value that fits the growth rate allowed by the culture medium under drug-free conditions (see the SI). Otherwise, decreases in can be calculated to reflect nutrient consumption, such as in saturating liquid cultures or as in the nutrient gradients generated by spatial structure in biofilms [7].

According to the framework of the proteome partition, the fraction of the proteome dedicated to ribosomal proteins varies linearly with the cell growth rate, from when to a theoretical maximum , since the remaining of the proteome is fixed and not affected by changes in metabolism [41]. Therefore, the difference between maximal and minimal ribosomal fraction is the variable part of the proteome that can be occupied by the sector proteins that are affected by translation inhibition and nutrient quality. The fractions of the proteome dedicated to ribosomal sector and variable sector proteins are given by , and , respectively, such that . The cell growth rate is proportional to the product of ribosomal content and translation capacity, and is calculated as , where is the conversion factor between RNA/protein ratio and ribosomal fraction calculated for E. coli.

Since expression of TetA and TetR has been shown to depend on cell growth, we assume these proteins belong to the variable sector . Therefore, without regulation of the synthesis rates and , we would expect the concentrations of TetA and TetR to scale by . We can then calculate the dependence of TetA and TetR synthesis on both translation inhibition and nutrient levels. This dependance is composed of two factors, one reflecting changes in growth rate and another reflecting changes in proteome partition. ( scales down gene expression to match the decrease in growth rate, which does not change expression levels. For proteins in the sector, there is further modulation by a factor , where is the -sector fraction under full nutrients and no drug. Therefore, the global metabolic effects on the expression rates of -sector genes can be modeled by . This leads to expression level steady states proportional to , as expected for proteins in the P sector (see dependence above) and simplifies to at full nutrients and no drug. We note here that although reducing either the nutritional or translational capacities result in decreased growth rates, they have opposite effects on the proteome partition. Therefore, while reducing the growth rate by nutrient limitation results in ribosome downregulation and increased TetA and TetR expression levels, reducing the growth rate by tetracycline exposure results in ribosome upregulation and decreased TetA and TetR levels. Next, we use our model to simulate the tetracycline response under different nutrient conditions and drug concentrations.

We begin by analyzing the time course of a typical response to a sudden exposure to tetracycline (figures 1(b)–(g)). Initially, as TetA levels are low, the drug quickly diffuses into the cell and accumulates in the cytoplasm, reducing the cell growth rate and slowing down gene expression. As the incoming drug quickly binds and inactivates repressor TetR, expression of both TetR and TetA is released shortly after exposure, although initial accumulation is slow. As TetA levels begin to increase in the cell membrane and export tetracycline back out of the cell, drug accumulation in the cytoplasm slows down and eventually reverses. As intracellular drug levels decline, cell growth and gene expression recover, accelerating TetA accumulation. When intracellular drug returns to low levels, TetR is released, resuming repression. TetA, TetR and tetracycline then equilibrate to steady-state levels, which depend on both TetR regulation and on the effects of the proteome partition on gene expression. This time course of the response dynamics qualitatively reproduces experimental measurements of expression of resistance genes and cell growth (figures 1(c)–(f)), obtained in a resistant population of E. coli cells suddenly exposed to a large dose of tetracycline in a microfluidic device [6, 57] (data obtained from [6]).

To understand how tetracycline concentration affects cell growth and survival, we simulated the drug response to exposures of increasing drug doses. As drug concentration increases, the growth reduction experienced by the cell at the beginning of a response also increases in both duration and magnitude (figures 1(h)–(j)). At high drug concentrations, synthesis of TetR and TetA is also significantly reduced during this state of translational inhibition, bringing the cell to a quasi-arrested slow growth state. This state can be escaped if the cell maintains cell growth, however slow, to eventually accumulate TetA to sufficient levels to kickstart drug export (figure 1(i)). With enough TetA, the cell enters a positive feedback loop where reduced intracellular drug concentrations leads to higher growth rates and faster TetA production, resulting in further reduction of intracellular drug levels and faster cell growth. As the drug dose increases further, the cell is trapped in the slow growth state for increasingly longer times before eventually recovering. At very high drug doses, however, recovery is no longer possible, with the cell reaching sufficient translational inhibition such that TetA is not produced at high enough rates to initiate a recovery (figure 1(j)). The cell then cannot counteract the influx of drug, causing the growth rate to be further reduced by the same positive feedback mechanism.

Increases in drug concentration result in longer recovery times, defined as the time it takes for the cell to recover to the average of its minimum and final growth rates, up to a threshold drug concentration where the recovery time tends to infinity (figure 1(k)). Past this threshold, the cell is permanently arrested following exposure and does not recover. We next determined the stable growth rates at the end of the antibiotic response for different doses of tetracycline, to examine the effect of the drug during steady state. Increasing drug doses cause a reduction in steady-state growth, while still keeping it at relatively high levels up to the threshold drug dose (figure