Quantum optomechanics is the field of research that studies the interplay between mechanical motion and light, at the quantum level [1]. The field has flourished over the past few decades, since progress in nano-fabrication technologies and cooling techniques has made possible reaching the regime in which quantum fluctuations represent the predominant source of noise and have sizeable effects on the dynamics of mechanical resonators [2–4]. Optomechanical systems are nowadays among the most promising platforms for the development of future quantum technologies [5]. They can be used for example in metrology, as ultra-high-precision sensors and actuators of nano-metric motion [6], and have been recently proposed as a platform to implement quantum thermal machines [7–11]. Remarkably, thanks to their exceptionally long coherence time [12, 13], quantum-enabled acoustic resonators represent a promising alternative to superconducting circuits for quantum information storage [14, 15] and processing [16]. It is clear that underpinning the use of these systems in quantum technology is the ability to exploit the coupling with optical or microwave radiation field to transfer information in and out of the acoustic resonators, thus implementing coherent control of mechanical vibrations at the level of few or even single quantum excitations [17, 18]. It is thus crucial for the research community to develop accurate theoretical models that describe the dynamics of nano-scale devices and their interaction with the radiation field.

At a more fundamental level, quantum fields interacting with movable boundary conditions provide a convenient framework to investigate the physics of the quantum vacuum and its instability in certain physical conditions. As originally demonstrated by Moore [19], Fulling and Davies [20, 21], the vacuum fluctuations of a quantum field can be converted into pairs of real photons by the non-adiabatic motion of a boundary condition (mimicking an ideal, perfectly reflecting mirror). This effect is known in the literature as dynamical Casimir effect (DCE) [22, 23] and has been extensively investigated in the literature (see topical reviews, such as [24–26]). The physical mechanism that engenders the dynamical Casimir emission is equivalent to the process by which particles are created in an expanding Universe, as anticipated by Parker [27, 28], and is related to the evaporation of black holes by the emission of Hawking radiation [29, 30]. In spite of the impressive recent technological advances in optomechanics, experimental evidence of the excitation of the electromagnetic vacuum, triggered by mechanical motion, has so far evaded observation. Experimental evidence of the DCE has been achieved instead in the context of analogue models based on superconducting circuit-QED [31, 32], in which case the mechanical motion of the mirror is mimicked by modulating in time the effective electric length of a microwave cavity, at frequencies high enough to resonantly amplify the DCE signal to a sizeable amplitude [33, 34]. Beside superconducting electronic circuits, a plethora of different experimental schemes and systems have been proposed in the literature as platforms to investigate the analogue of the DCE. These include: all optical systems with periodically modulated effective cavity length [35, 36], Bose–Einstein condensates of ultracold atoms [37] with time-dependent atomic scattering length [38–42], quantum fluids of lights [43], hybrid atomic-mechanical systems [44] and supercooled membranes driven by time-dependent classical fields [45, 46].

According to its original formulation, the DCE is a test-field effect, meaning that the time-dependent boundary condition imposed to the field is not a dynamical degree-of-freedom of the system, but is a mere external parameter. In a real optomechanical system instead, the mechanical objects that interact with radiation are engendered with their own quantum dynamics and the effects of the back-action (back-reaction) of the quantum field onto the mechanical motion need to be taken in to account [47]. In static configurations, early works [48–51] have studied the modification of the ground state of an optomechanical system, due to the quantized motion of the optical mirror, while the role of the quantum vibration of an acoustic resonator as mediator of the interaction between two physically separated fields have been recently investigated in [52]. Further studies investigated out-of-equilibrium configurations, demonstrating that the electromagnetic vacuum is able to affect the motion of mechanical objects [53], inducing dissipation and fluctuations [54–60], as well as quantum decoherence [61–63]. Such decoherence effects are responsible for driving the quantum-to-classical transition of any macroscopic objects interacting with light [64]. Pioneering theoretical works pushed these studies towards more complex configurations, proving vacuum mediated coherent exchange of excitations at the single phonons level between physically separated mirrors [65, 66] and between mirrors and atoms [67], as well as photons hopping induced by mechanical zero-point fluctuations [68] in optomechanical lattices [69].

This paper adds to the existing literature, with the objective of setting up the formalism to address the back-reaction by DCE, adopting an open quantum system approach to the problem. This approach is analogous to the one developed in [61, 62, 70, 71], but makes use of the more refined microscopic model developed in [72], to describe the interaction between mirrors and light. By using this model, we are able to account for the dielectric properties of the mirror from first principles, achieving a description of the interaction beyond the standard theory of radiation pressure [73, 74], which relies on unphysical boundary conditions enforcing the field to vanish in correspondence of the mirrors. This naturally leads to an ultraviolet cut-off in the theory, thus solving the pathologic ultraviolet behaviour that plagues standard theory of radiation pressure in the case of the multi-mode field configurations [48–52]. For simplicity, we develop a one-dimensional (1D) model, so that the electromagnetic vector potential can be treated as a scalar field. Despite this simplifying assumption, we expect that the theory we present is able to capture all the relevant qualitative features of the back-reaction. A similar study has recently been presented in [75], where the authors attempted to use the theory of the influence functionals in order to find an effective action for the mechanical motion of a mirror interacting with the radiation field. In our work, we pursue the same study by adopting the equivalent Hamiltonian formalism, and obtain results that differ from the findings presented in [75], in certain respects.

The paper is organized as follows: in section 2, we review the microscopic model proposed in [72], that we use to describe the mirror-field interaction. There, we consider the mirror being static, since the focus is on deriving the dielectric response of the mirror to radiation. The aim of this section is to set the notation and introduce the basic properties of the model. We do not dwell on the details of the model and on how this relates and generalizes other standard field-mirror interaction models. We refer the interested reader to the original work [72], where this model was first introduced, for a comprehensive discussion on this matter. In section 3, we consider the case of the mirror vibrating within a confining harmonic potential, and present the Hamiltonian that describes its dynamics. In section 4, we use perturbation theory to derive the master equation for the reduced density matrix of the mirror and introduce key physical quantities, such as the noise and dissipation kernels, that describe the back-reaction effects of the field onto the mechanical motion of the mirror, at the microscopic level. This is the first major result of this paper. At the macroscopic level, the back-reaction appears in the form of an effective friction experienced by the mirror, as well as diffusion, the latter being responsible for quantum decoherence. Fluctuation and dissipation kernels are defined in terms of relevant physical properties of the environment in which the mirror is located (i.e., the field and the microscopic degree-of-freedom that mediates the interaction), that are encoded in the correlation functions calculated in section 5. Specifically, in sections 5.1 and 5.2, we determine the correlation functions for the field and the internal degree-of-freedom of the mirror, while in section 5.3 we present the explicit expressions for the noise and dissipation kernels for the mechanical motion of the mirror, which are the second key result of this paper. Our findings for the structure of these kernels differ from the corresponding ones presented in [75]. Incidentally, we show that noise and dissipation kernels for the mechanical motion of the mirror are related by standard fluctuation-dissipation relations (FDRs), as expected. Such relations are not found in [75], where the authors introduce instead certain generalized relations. Furthermore, we give evidence that the back-reaction onto the moving mirror is associated with the emission of pairs of particles by DCE. In section 6, we present the master equation both in the position and Wigner representation, and discuss in more details the physical processes it accounts for. Our conclusions are finally drawn in section 7.

Let us consider the 1D system composed by a moving mirror of mass M, confined within a harmonic potential of frequency Ω, interacting with the scalar field φ. We indicate by X the degrees-of-freedom corresponding to the mechanical displacement of the mirror. By following [72], we assume that this coupling is mediated by an internal degree-of-freedom (idf) of the mirror, whose dynamics is modelled as a harmonic oscillator q of mass m and frequency ω0. Specifically, we model the interaction between the field and the idf in terms of a bilinear (i.e. linear in the corresponding variables) coupling. This system is sketched in figure 1. By taking into account the microscopic dynamics of the mirror, this model is able to describe basic dielectric properties of optical mirrors, such as their transparency to radiation at high frequencies. This allows us overcome issues related to the standard theory of radiation pressure commonly used in optomechanics [73, 74], according to which the interaction results from (unphysical) boundary conditions that force the field to vanish at the location of the (ideal) mirror. As discussed in [72], this theory generalizes and includes as subcases other popular optomechanical models [76–79], including the standard optomechanical coupling , where is the number operator of field excitations impinging on the mirror and is the position operator of the mirror itself [1]. As such, the approach we pursue is more general and aims towards a more complete theory of optomechanics. For the sake of completeness, we briefly describe in this section the main features of the model we use, and show how the internal dynamics of the mirror determine its response to radiation. The content of this section closely follows [72], to which we direct the interested reader for more details and for a comprehensive discussion on how this theory relates and improve standard optomechanical models.

Figure 1. Schematic representation of the system: The optical mirror of mass M is confined by a harmonic potentials of frequency Ω. Its displacement from the equilibrium position is indicated by the coordinate X. The mirror interacts with a scalar field via the mediation of the internal harmonic oscillator q, whose characteristic frequency is ω0, while its mass is m.

Download figure:

The dynamics of the full system is described by the following action:

Throughout this paper we use the standard notation and indicate total time derivatives with dots over symbols, while c is the speed of light. The first three terms in equation (1) account for the free evolution of the field, of the mechanical oscillations of the mirror and of the idf, respectively, while the last term describes the bilinear coupling between the idf and the field. Notice that, in the latter term, the delta function enforces the interaction to take place at the position of the mirror, and thus couples implicitly all the degrees-of-freedom of the system. We indicated by λ the interaction strength. In the rest of this section, we discuss the response of the mirror to the field, in terms of its transmittivity and reflectivity properties. To this end, we freeze for the time being the mechanical motion and assume the is mirror at rest at the bottom of the confining potential. We use coordinates such that this equilibrium position is at x = 0. The frequency-dependent reflection and transmission coefficients are obtained from the equations of motion for the idf and the field, which can be deduced by varying the action, with respect to q and φ. These take the form:

From equation (2), we infer that the first spatial derivative of the field is discontinuous at the mirror's position, but the field itself is continuous at the same point. To determine the spectral response of the mirror to radiation, let us consider the plane wave φω of frequency ω, incident from the left and scattered at the mirror's position. The spatial structure of this field mode has the form:

where is the standard Heaviside function and we defined the field on the left and on the field on the right of the mirror, as:

The field is the linear combination of the right-moving incident plane wave and the left-moving reflected component, while represents the transmitted component. Since the mechanical fluctuations of the mirror are frozen, the interaction involves only the field and the idf, and is quadratic. Thus, in the steady state, the idf oscillates in time with the same frequency of the field: 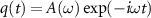. The amplitude of the idf oscillations is obtained by substituting this expression into equation (3), together with the field evaluated at the location of the mirror: (remember that the field is continuous across the mirror). The amplitude of idf oscillations are then obtained in the form:

The continuity of the field and the discontinuity of its spatial derivative at the mirror's location, provide us with the two conditions needed to determine the frequency-dependent reflection and transmission coefficients. In particular, the jump of the spatial derivative of the field across the mirror is obtained by integrating the equation of motion equation (2) over an infinitesimally small interval encompassing the mirror. These conditions give us the following set of equations:

Upon substitution of equations (5) and (6), and given the steady state form for q(t) given above, with the amplitude as specified in equation (7), these conditions give us the following closed set of equations:

from which the transmission and reflection coefficients are obtained in the form:

The squared modulo of these coefficients can be conveniently written by using the auxiliary function , as:

where is the plasma frequency that characterizes the internal oscillations of the mirror. For illustrative purpose, equations (14) and (15) are plotted in figure 2, for different values of the ratio . As evident from the figure, and discussed in details in [72], the relative value of the plasma frequency respect to the frequency of the idf specifies the operating regime of the mirror: In the case ( in figure 2), the reflection coefficient is sharply peaked in a small interval around the idf frequency, so that the mirror reflects the incident radiation in a narrow bandwidth centred at ω0. In the opposite limit instead ( in the same figure), the mirror reflects the incident radiation over a much broader low-frequency bandwidth. These results demonstrate that the model is able to account for the partial reflectivity properties of real optical mirrors, and correctly captures its transparency to high-frequency radiation. We can take the characteristic frequency at which this transition happens as the one at which . In such conditions: , inspection of which gives the scaling , in the limit .