Objective. Multiple algorithms have been proposed for data driven gating (DDG) in single photon emission computed tomography (SPECT) and have successfully been applied to myocardial perfusion imaging (MPI). Application of DDG to acquisition types other than SPECT MPI has not been demonstrated so far, as limitations and pitfalls of current methods are unknown. Approach. We create a comprehensive set of phantoms simulating the influence of different motion artifacts, view angles, moving objects, contrast, and count levels in SPECT. We perform Monte Carlo simulation of the phantoms, allowing the characterization of DDG algorithms using quantitative metrics derived from the data and evaluate the Center of Light (COL) and Laplacian Eigenmaps methods as sample DDG algorithms. Main results. View angle, object size, count rate density, and contrast influence the accuracy of both DDG methods. Moreover, the ability to extract the respiratory motion in the phantom was shown to correlate with the contrast of the moving feature to the background, the signal to noise ratio, and the noise in the data. Significance. We showed that reporting the average correlation to an external physical reference signal per acquisition is not sufficient to characterize DDG methods. Assessing DDG methods on a view-by-view basis using the simulations and metrics from this work could enable the identification of pitfalls of current methods, and extend their application to acquisitions beyond SPECT MPI.

Respiratory motion correction plays a pivotal role in improving image quality in single photon emission computed tomography (SPECT), enhancing diagnostic accuracy (Werner et al 2009, Pretorius et al 2020, Robert et al 2022) and facilitating quantitative uptake analysis (Kortelainen et al 2021). Since hardware-driven respiratory motion correction methods have not been adopted widely in clinical practice (Iyer et al 2021, Pretorius and King 2021, Grootjans et al 2022), various data driven gating (DDG) approaches have been proposed for SPECT that derive respiratory surrogate signals from data directly (Kyme and Fulton 2021). Moreover, Siemens Healthineers recently introduced respiratory motion correction in their Symbia Pro.spectaTM SPECT scanner, meaning that respiratory motion correction is now routinely applied to patients undergoing SPECT Myocardial Perfusion Imaging (MPI). The algorithm underlying respiratory motion correction on the Symbia Pro.spectaTM uses the non-linear manifold learning method Laplacian Eigenmaps (LE) and has been shown to have a mean correlation of 0.87 to a physical reference for SPECT MPI studies on a previous SymbiaTM T2 SPECT machine (Sanders et al 2016).

Multiple other algorithms have been proposed for DDG, employing different methods for obtaining a respiratory surrogate signal. Pretorius and King (2021) proposed tracking the COL (also referred to as center of mass) of a masked subset of the projection data to extract a respiratory surrogate signal and reported an average correlation of 0.7 to a physical reference. Garmendia et al (2021a, 2021b) proposed an approach that extracted a respiratory surrogate signal from projection data using a (regularized) maximum likelihood estimation (MLE) algorithm and reported a mean correlation of 0.89 to a physical reference in their latest work. Recently, a deep learning (DL) based method has also been proposed for DDG and has been shown to have a mean correlation of 0.9 to a physical reference in MPI (Chen et al 2022). All methods mentioned before have been shown to work well for SPECT MPI, but have not been applied to other acquisition types, or were shown to have worse performance for those, e.g. as shown by Sanders et al for SPECT lung and shunt imaging (Sanders et al 2016).

We found that the current method of evaluating DDG may not be adequate, as the performance of the methods is expressed as mean correlation to an external physical reference per acquisition. This fails to capture the limitations that the methods might have. Within a given view, there can be discrepancies between the motion of the gall bladder and the myocardium (Reymann et al 2022), while bulk patient motion can be superimposed with respiratory motion. Over the course of an acquisition, depending on the view angle, different organs dominate the information on the detector, in addition to changes in the biodistribution of the tracer. Moreover, limitations of hardware-based references may introduce further inaccuracies as typically only capture secondary effects of the respiratory motion.

Therefore, a more comprehensive analysis of the current limitations of DDG methods under various imaging conditions, such as varying injected activities, uptake ratios in different structures, acquisition angles, sizes of moving structures, and motion patterns in the absence of influences seen in patient data, is needed. This could be achieved by using Monte Carlo simulation (MCS) with software motion phantoms and comparing the algorithms given the simulation parameters, which allows the separation of additional factors from the baseline performance of the methods. To the best of our knowledge, there are currently no methods or datasets published that allow this kind of comparison and thus enable the development of a method allowing DDG for further SPECT acquisition types.

In this work, we develop a method for creating a water cylinder phantom combined with a moving sphere that represents respiratory motion and allows the simulation of arbitrary scenarios composed of different motion patterns and amplitudes, injected activities, and contrast ratios between sphere and background. We derive metrics to correlate the observed data at the detector with the outcomes of DDG algorithms and probe the method by comparing COL and LE as sample DDG methods.

2.1. Water cylinder phantoms

To facilitate characterization of different DDG methods without the influence of external effects such as bulk patient motion, changes in activity distribution, and inaccuracies of the physical reference signal that could occur in patient data, we simulate a static water cylinder phantom with one or more moving spheres inside. For this, we use the specifications of the Jaszczak water cylinder and create the phantoms with a voxel size of 1 mm and a matrix size of 256 × 256, representing a volume of 6477 ml. We simulate phantoms with different motion patterns by adding a sphere with varying position, motion, diameter, and contrast to the water cylinder. Respiratory motion was simulated as a sinusoidal axial translation of the sphere with amplitude ±5 cm and a rate of 14 bpm for 15 s duration using the neurokit library (Makowski et al 2021). We note that in order to obtain projection data with realistic motion, the phantoms need to have sufficient spatial and temporal resolution. Consequently, we create phantoms every 200 ms during the motion, resulting in 75 time steps (based on 64 distinct amplitude positions) for the τ = 15 s motion signal used. In spatial dimension a recommended pixel size for SPECT MPI is 6.4 mm (Dorbala et al 2013) but can be as low as 2.4 mm when using a Siemens Healthineers SPECT systems with a 256 matrix (Sanders et al 2016). This requires a smaller voxel size to allow for sub-pixel motion, which is why we chose a 1 mm voxel size. We simulate three different motion scenarios: the water cylinder with one moving sphere at the center (scenario: baseline), one static sphere and one moving sphere (scenario: static sphere), and one off-center sphere moving according to the aforementioned motion plus one central sphere with a higher-frequency motion of 20 bpm and amplitude ±3 cm (scenario: motion sphere). This means that the DDG methods in the baseline scenario are only extracting the motion of the single sphere with no interference from surrounding objects, since there is only static background. By contrast, in the static or motion sphere scenario, the second sphere—either stationary or moving—introduces motion effects from these neighboring objects.

For each scenario, we simulate different combinations of sphere diameter (d ∈ [9.5, 12.7, 15.9, 19.1, 25.4, 31.8] mm), geometric variance by placing the spheres at different x-positions (x ∈ [0, 2, 4, 6, 8] cm off-center), and different contrast ratios of the spheres s to background b (b ∈ [10, 200, 400, 800, 1000] kBq ml−1), where the sphere to background ratio s: b in ∈[1, 3, 5, 7, 9]: 1. Figure 1 shows a sample frame of the water cylinder phantom with two spheres.

Figure 1. Sample water cylinder phantom with two spheres. Top left to right: simulation showing sphere S1, sphere S2, and background W. Bottom left: combined data I. Bottom center: combined data with mask in yellow, mask in green, and mask MW in red. Bottom right: cross-section of the raw phantom with the two spheres of diameter 31.8 and 19.1 mm.

Download figure:

Standard image High-resolution image

Practically, we simulated a total of 64 (amplitude positions) ×5 (x-positions) ×6 (sphere diameters) +1 (water cylinder) = 1921 distinct phantoms, that were then combined into 1 170 000 simulations (see table 1).

Table 1. Overview of simulated phantom combinations.

ScenarioBaselineStatic sphereStatic sphereMotion sphereDiameter S1 [ mm]ΩΩΩΩDiameter S2 [ mm]—19,119,1Same as S1 x-position S1 [ cm]0, 2, 4, 6, 802, 4, 6, 80 x-position S2 [ cm]—2, 4, 6, 802, 4, 6, 8Contrast S1ΓΓΓΓContrast S2—ΓΓΓViews120120120120Activity level [kBq ml−1]ΨΨΨΨResulting num. simulations90 000360 000360 000360 000 Total simulations1170 000

This table provides an overview of the simulated phantom combinations. In this context, the symbol Ω represents the different diameters of sphere 1, which include [9.5, 12.7, 15.9, 19.1, 25.4, 31.8] mm. The symbol Γ denotes the contrast to background ratios, comprising [1, 3, 5, 7, 9]. Additionally, Ψ stands for the various activity levels, encompassing [10, 200, 400, 800, 1000] kBq ml−1. The simulations for the static sphere are presented in two separate columns for better clarity.

2.2. Monte Carlo simulation

We perform high-count simulations of the spheres and background compartments separately and then perform a weighted combination of the regions followed by applying Poisson noise post-simulation, as presented by Ghaly et al (2014). This noise is introduced using distinct random seeds for each simulation.

Simulations were performed using the simulating medical imaging nuclear detectors (SIMIND) program (Ljungberg 2018) version 6.2, simulating Tc-99m using the siemens healthineers symbia low energy high resolution (LEHR) collimator definition contained in SIMIND at a constant radius of rotation of 30 cm. For the sphere study, we simulated 120 views, distributed evenly over 360◦, rotating counter-clockwise around the x-axis of the three-dimensional (3D) phantom starting with the 0◦th view, shown on the bottom right of the figure 1. Data were scaled to the desired temporal resolutions of 200 ms by normalizing the high-count simulation to and then multiplying by 0.2 s. The different contrast ratios s: b were simulated by performing a weighted combination of the simulated regions (Reymann 2023).

2.3. Data driven respiratory gating

As sample DDG methods, we compare the COL method representing a linear Dimensionality Reduction (DR) method, and LE representing a non-linear DR method. For both methods we first 3D filter the data with a box kernel of spatial dimension 32 × 32 and temporal dimension 2 to reduce the noise in the data. The COL method uses the weighted center of light along the body axis, to get an estimate of the respiratory motion in the data. We use this method without any thresholding or masking, to visualize the effects of other structures in the projection data. The LE method was implemented as described in Sanders et al (2016), using the adaptive heat kernel to compute the affinities of the vectorized projections.

Different means of post-processing of the extracted noisy respiratory surrogates have been proposed for the different methods, including adaptive normalization, flipping, shifting, and smoothing. To obtain an unbiased comparison between the methods, we omit method-specific post-processing and restrict post-processing to Savitzky-Golay filtering with a span of nine and an order of three. We report the absolute value of Pearson's correlation coefficient ∣ρ∣ between the smoothed estimate and the ground truth. Note that we use the absolute of ρ, as the eigenvector-based methods might return a surrogate signal with incorrect polarity, which can be addressed by an appropriate post-processing method but does not actually influence the goodness of fit of the extracted surrogate.

2.4. Evaluation

To characterize under which imaging conditions the different DDG methods perform optimally, we propose several metrics that describe the count statistic independently for each view angle v. Since we use simulated data in this work, we can access the count contributions to the observed image data I(x, y, t) at position (x, y) and time t, consisting of the counts of all objects O as

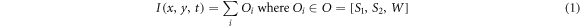
(see figure 2). For the baseline scenario, this implies that the observed counts I consist of the combined counts Ow from the water cylinder and the counts O1 from sphere 1, represented as I = Ow + O1. To analyze statistics within certain regions on the detector, we define masks:

Figure 2. Visualization of phantoms, masks, and simulations for one timepoint t and view angle v. The individual phantoms O are forward projected to obtain the masks M. For each view v and timepoint t simulations are obtained via SIMIND. The counts are only measured within the mask, shown on the right-most column. A combination of all observed data is shown in the bottom row below the blue line. To create the input for the DDG algorithms, 75 different timepoints t with different phantom positions are simulated.

Download figure:

Standard image High-resolution image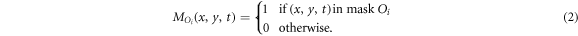

We calculate the counts emitted by an object that are measured within its mask as

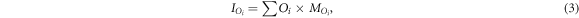
for example, the counts emitted by sphere 1 and measured within sphere mask 1 are referred to as , while denotes the counts emitted from the water cylinder and measured in the background region.

We can then compute the count rate density in unit in the different masks by normalizing with the mask area a and the time duration τ, resulting in the count rate densities:

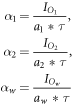
for sphere 1, 2, and background, respectively.

Next, we measure the signal to noise ratio (SNR) in the different image regions by calculating the ratio

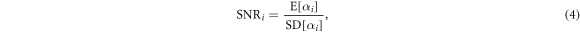
where E[X] refers to the mean and SD[X] to the corrected sample standard deviation of X. For regions with low noise, this ratio will approach a larger value, and for low count levels, the value will decrease.

We compare the performance of the DDG methods by computing the mean correlation for a given metric, e.g. SNR, and compare it to an ideal method (always resulting in ρ = 1). We compute a recovery coefficient r, indicating the goodness of the methods over all simulations, by comparing the area under the curve (AUC) of the DDG method with the ideal method

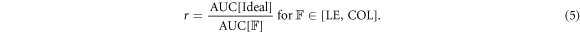
In all figures, we visualize the uncertainty of the data by plotting error bars for the different metrics, where the Standard Error (SE) is defined as the standard deviation divided by the square root of the sample size.

In the baseline artifact-free simulation with only one moving sphere, a relationship between the simulation parameters and the accuracy of the DDG methods can be seen. The most dominant influence was seen by the sphere diameter, which is shown in figure 3 along with two sample respiratory estimates, on average resulting in correlations ∣ρ∣ ranging from as low as 0.37 for spheres of diameter 9.5 mm to 0.80 for spheres with diameter 31.8 mm for the LE DDG method. We also show the influence of other simulation parameters, such as view angle, contrast of the sphere to background, total simulated activity, and distance of the sphere to the center of the water cylinder phantom in figure 4.

Figure 3. Left panel shows the influence of the sphere size on the mean accuracy of the DDG methods for the baseline scenario along with the SE. The right panel shows two sample respiratory signal estimates using the LE method for a simulation with parameters: v: 96◦, x: 8 cm, s: b = 3: 1, and b: 200 kBq ml−1 for two different diameters along with the ground truth signal.

Download figure:

Standard image High-resolution image

Figure 4. Influence of different simulation parameters on the accuracy of the DDG methods for the baseline scenario. Each plot shows the mean correlation of N = 90 000 simulations given the simulation parameter on the x-axis versus the correlation ρ to the ground truth along with the SE indicated with error bars.

Download figure:

Standard image High-resolution image

The first plot shows that the accuracy for both DDG methods changes depending on the view angle, due to the motion sphere being off-center for the majority of simulations. Similarly, the contrast of the sphere to the background, the total simulated activity, and the distance of the sphere to the center of the water cylinder phantom influence the data seen on the detector and therefore the accuracy of the extracted respiratory surrogate signal. The mean ± SE of the correlation for all simulations shown in figure 4 was 0.56 ± 8.22 × 10−4 and 0.43 ± 8.14 × 10−4 for LE and COL, respectively.

In figure 5 we show the relationship of the different metrics with the accuracy of the extracted respiratory surrogate for the static and motion sphere simulations. The plots were created by splitting the metrics into bins with an equal number of samples (N = 100) and then computing and plotting the mean correlation and SE for each bin. We also show the response of an ideal method that would result in a correlation of 1.0 regardless of the value of the metrics, which we use to compute a reference AUC. The recovery coefficient r is computed with respect to this reference AUC and is also shown in the legends for each method, where a larger r represents a more precise method.

Figure 5. Mean correlation ∣ρ∣ of the extracted respiratory surrogate signals with the ground truth motion for the different scenarios simulated. Columns show the different scenarios: baseline, static sphere, and motion sphere, rows show correlation versus the count rate density ratio in the first row and the SNR1 of sphere 1 in the second row. The legends indicate the recovery coefficient r and significant differences (*) between the methods (p < 0.01).

Download figure:

Standard image High-resolution image

For both DDG methods and in all simulated motion scenarios, there exists a positive correlation between the count rate density ratio and the SNR to the accuracy of the extracted respiratory surrogate, respectively.

Figure 5 shows that in general, the more counts come from the region of interest, the more likely the methods return a motion agreeing with the ground truth. Similar to the baseline scenario, there exists a positive correlation between the count rate density ratio and the SNR to the accuracy of the extracted respiratory surrogate for the motion sphere simulations, although there is more uncertainty.

The experiments shown in this work demonstrate that many parameters influence the accuracy of DDG. The use of water cylinder phantoms with a moving sphere inside represents a simple imaging scenario that excludes motions from other surrounding structures that is unrealistic to achieve with anthropomorphic phantoms or patient data. This allows the characterization of a method's response to different feature sizes, contrast ratios of feature to background, and count levels.

Through the simulations, we showcased that, apart from the distance to the detector, all simulation parameters significantly impacted the precision of DDG methods. Previous work has shown that the amount of activity injected, and hence the contrast of the organs to the background, correlates with the accuracy of DDG methods, which we confirmed with our simulations (Sanders et al 2016, Pretorius and King 2021). However, we also showed that other effects, such as feature size or acquisition angle, play an important role in extracting accurate respiratory signal estimates. In the baseline scenario, the overall mean accuracy for the LE method was found to be 0.56. However, the mean accuracy varied significantly depending on the acquisition angle, as determined by a one-sample t-test with a significance level of p < 0.01. For instance, at acquisition angle 78◦, the mean accuracy was 0.62, whereas at acquisition angle 246◦, the mean accuracy was 0.48 (also see figure 4).

Through simulating a baseline scenario without other 'noise' influences (such as bulk patient motion or extra activity), we established a baseline performance for the various DDG methods and highlighted the impact of artifacts on their performance. Upon introducing a second sphere with different motion in the simulations, both the LE and COL methods exhibited a decrease in the recovery coefficient. Our findings also showed that regional image characteristics, such as the count rate density ratio and the SNR of the region of interest, serve as reliable indicators for the feasibility of DDG. The results of this experiment could be used to define lower thresholds for performing DDG, e.g. by excluding acquisitions with as the mean correlation for these simulations was on average <0.85, irrespective of method or scenario simulated. Similarly, a SNR of could be used as lower limit for performing DDG.

In this work, we choose a sphere as the moving object, representing a trivial geometric object that does not introduce any shape dependencies to the simulations. We chose to simulate SPECT acquisitions, but this method is also applicable to any other Emission Tomography modality, where the same metrics (count rate density and SNR) can be computed at the detector level. Unlike previous methods (Sanders et al 2016), we do not combine data from multiple detectors, allowing the assessment of the DDG for each view independently. We simulated many, but not all combinations of the water cylinder phantoms, e.g. leaving out smaller spheres for combinations of the motion sphere simulations, due to the amount of data that would have to be generated. In theory, over 40 million different combinations could have been simulated based on the degrees of freedom allowed by our phantoms but were not computationally feasible. Moreover, we did not simulate the influence of different motion amplitudes and frequencies in this work, and it is unclear if the motion of larger objects with low amplitude, or the motion of objects with high amplitude may not be detectable. Simulations involving different motion patterns and more parameter combinations would provide further insight, and we believe that the metrics derived in this work can also be used to characterize these simulations. In the context of conventional SPECT MPI studies, where the focus is on the moving heart and cationic Technetium 99 m (Tc-99m) complexes are employed as tracers (Klein et al 2020), our simulation work involves smaller objects (≤31.8 mm) compared to the human heart (sized between 60 and 120 mm) (Gordon Betts et al 2021). Additionally, we simulated these objects with a wide range of activity levels (ranging from 10 to 1000 kBqml, equivalent to 64.7 MBq–6.47 GBq for our phantom volume), in contrast to the clinically administered doses (ranging from 350 MBq–1.1 GBq) (Klein et al 2020). We chose these to probe cases of lesion size and activity that would challenge the performance of the algorithms. As also seen in figures 3 and 4, when simulating smaller objects with lower contrast and lower simulated activity, both methods are in their breakdown regime, and improvements of the methods could be possible. This explains why the average results in this work are lower compared to previous publications.

Using the SIMIND MCS introduces a simplification to the image formation model, as SIMIND employs acceleration techniques like variance reduction, and Poisson noise is only applied post-simulation, however, we are not interested in the specific physics of the simulation and consider the generated data accurate enough for the purpose of DDG (Bahreyni Toossi et al 2010). This extends to the metrics used to measure the local count statistics, which have been shown to correlate with the ability to predict the outcome of the DDG methods. The metrics confirm our experience, that with more counts (hence less noise), the extracted respiratory surrogates are closer to the ground truth. Furthermore, higher contrast between feature and background improved correlation to the ground truth and can be measured as the ratio of the count rate densities. The use of the recovery coefficient allows the comparison and application-driven design of new DDG methods, as it captures the performance and accuracy of DDG methods across the entire spectrum of possible observed data. Since we used simulated data in this work, it was possible to access the actual ground truth count rate densities of the different simulated objects to derive accurate projection-level statistics. Although this is not possible in real patient data, one can compute statistics on real data using (automated) segmentation methods (Mürschberger et al 2020) to compute the local statistics.

As a proxy for DDG algorithms, we used the COL and LE methods in this work, representing a linear and non-linear method, respectively. Both methods use all available data as input and therefore showed a reduced accuracy when artifacts are present in the data. Using methods that mask out certain parts of the data might help improve the robustness of the extracted surrogate signal. Moreover, it remains unclear how DL methods perform on this simulated dataset, in particular when they were trained on simulated data that contains artifacts. We plan on investigating the use of masking and DL for DDG in future work.

We demonstrated that evaluation of DDG algorithms for SPECT expressed as mean correlation to an external physical reference per acquisition is not sufficient for characterization of the algorithms' performance. Both COL and LE DDG methods were influenced by contrast, count level, noise, and SNR, which can change from view to view. To establish DDG for other examination types, the metrics presented in this work can be used to identify the constraints and pitfalls of DDG algorithms and guide the development of new approaches. An analysis of DDG methods using MCS of the proposed phantoms allows for the differentiation between the decreased precision originating from external sources, and the proficiency of the methods in extracting a correct respiratory surrogate signal in general.

The data that support the findings of this study are openly available at the following URL/DOI: https://doi.org/10.5061/dryad.n8pk0p313. Data will be available from 12 April 2023.