We employed mathematical models of spontaneous and stimulation-evoked neural dynamics to identify pulse sequences that minimize the 2-norm of frequency-specific neural activity. The 2-norm of a signal is equal to its energy, which is the integral of its instantaneous power with respect to time. Therefore, by minimizing the 2-norm of a frequency-specific signal, we are minimizing its overall energy. The average power, typically used in neuroscience to measure the size of neural signals, is not used in this study because it is not a norm or used in established optimization methods. We considered a generalized mathematical model in which relevant parameters of the stimulation-evoked responses (i.e. damping and natural/resonant frequency) were varied in order to understand whether the identified pulses patterns can be applied to distinct neural dynamics. To understand whether our results with the generalized model could be used to modulate more complex, neural dynamics similar to those observed in-vivo, we identified optimal pulse sequences for a mathematical model of spontaneous and stimulation-evoked activity in the GPi derived with data recorded from a PD patient [14]. We considered electrical stimulation waveforms that consist of a negative followed by a positive square pulse. These two square pulses have the same amplitude and a constant pulse width (i.e. symmetric, biphasic waveform). The pulse width is equal to the sampling period used in the discretization of the evoked response mathematical model.
The effect of stimulation pulses on the neural evoked response temporal dynamics was characterized using a saturation nonlinearity (static) connected to a system of linear equations of differences (discrete time approximation of differential equations) as depicted in figure 1. This generalized model structure has been shown to approximate the linear response of neural circuitry to electrical stimulation pulses [12, 14]. The saturation nonlinearity takes a biphasic pulse and converts it into a monophasic cathodal pulse (negative phase), which dominates the neural response according to experimental data [12]. Therefore, an alternative neural dynamics model can replace the saturation nonlinearity with pulses that are strictly monophasic. Of note, the generalized model can be interpreted as a linear approximation (around equilibrium) of a mean-field neural model, typically used in neuroscience to study neuronal populations computationally or characterize neural circuits based on data [15]. The evoked response model is described by the following equations of differences
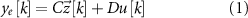
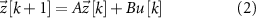
where 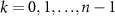 is the discrete time sample associated with time
is the discrete time sample associated with time 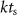 ;
; 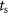 is the sampling time;
is the sampling time; 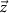 is the state vector;
is the state vector; ![$u[k] \lt 0$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn10.gif) is the saturated, monophasic input stimulus;
is the saturated, monophasic input stimulus; ![$y_e[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn11.gif) is the evoked response at sample k; and A, B, C and D are constant matrices that parameterize the equations of differences. In our model, D = 0 since there is no feed-through gain from the stimulus to the neural response. The saturated, monophasic stimulation input is given by
is the evoked response at sample k; and A, B, C and D are constant matrices that parameterize the equations of differences. In our model, D = 0 since there is no feed-through gain from the stimulus to the neural response. The saturated, monophasic stimulation input is given by ![$u[k] = \mathrm(\hat[k]-\underline)$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn12.gif) , where
, where 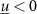 is an offset representing the minimum size stimulation that evokes a neural response,
is an offset representing the minimum size stimulation that evokes a neural response, 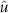 is the biphasic pulse, and
is the biphasic pulse, and 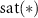 is the saturation operator that converts any positive value to zero. This operator is given by:
is the saturation operator that converts any positive value to zero. This operator is given by:
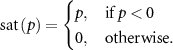
Figure 1. A schematic of the model dynamics capturing the interaction between spontaneous and stimulation-evoked neural activity in the targeted brain region. A biphasic stimulation pulse train, where each pulse is represented by a negative followed by a positive pulse, which after saturation is reduced to just the negative square pulse train. The saturated pulse train is responsible for evoking stimulation based oscillations, the dynamics of which can be mapped to a Toeplitz matrix ( ). The final model is the summation of the matrix multiplication of the
). The final model is the summation of the matrix multiplication of the  with the optimization variable vector (
with the optimization variable vector (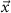 ) and the vector containing the spontaneous oscillations (
) and the vector containing the spontaneous oscillations ( ).
).
Download figure:
Standard image High-resolution imageThe LFP measurement, which reflects the combined spontaneous and stimulation-evoked neural activity, is modeled as
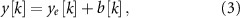
where ![$b[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn16.gif) is the value of the spontaneous neural oscillations at sample k. This linear model is a low-order simplification of the interaction between the spontaneous and stimulation-evoked neural activity that has been shown to be an approximation of experimental data [12, 14]. However, of note, this LFP model does not consider saturation effects associated with the finite number of neurons in the neuronal population being modeled, high-order nonlinear dynamics, or synaptic plasticity. The spontaneous oscillations (
is the value of the spontaneous neural oscillations at sample k. This linear model is a low-order simplification of the interaction between the spontaneous and stimulation-evoked neural activity that has been shown to be an approximation of experimental data [12, 14]. However, of note, this LFP model does not consider saturation effects associated with the finite number of neurons in the neuronal population being modeled, high-order nonlinear dynamics, or synaptic plasticity. The spontaneous oscillations (![$b[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn17.gif) ) were modeled using sinusoidal functions or synthetic LFP signals that match the power spectral density (PSD) of LFPs recorded from a PD patient.
) were modeled using sinusoidal functions or synthetic LFP signals that match the power spectral density (PSD) of LFPs recorded from a PD patient.
We used a second-order model of the evoked response to characterize optimal stimulation sequences that suppress or amplify spontaneous oscillations. The second-order model is given by equations (1) and (2). The following matrices describe the parameters of these equations [16]:
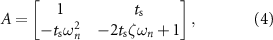



where 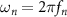 is the natural angular frequency (rad/sec) of the evoked response, ζ is the damping ratio, ku
is a scalar gain, and
is the natural angular frequency (rad/sec) of the evoked response, ζ is the damping ratio, ku
is a scalar gain, and 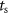 (sec) is the sampling period.
(sec) is the sampling period.
It's important to mention that any high-order mathematical model characterized by linear differential equations can be decomposed into multiple first and second-order models [17]. The second-order models, as the one described above, provide a description of the oscillatory modes in the dynamics being studied. Therefore, our analysis of a second-order system provides insights into the DBS sequences that need to be delivered to control neural dynamics driving oscillatory behavior. We considered two distinct signals to characterize the spontaneous oscillations (![$b[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn20.gif) ) in the generalized neural dynamics model. The first signal type is given by a sinusoidal function of frequency f0:
) in the generalized neural dynamics model. The first signal type is given by a sinusoidal function of frequency f0:
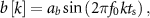
where ab is a constant that defines the signal amplitude. The second signal type is a sinusoidal function of frequency f0 whose amplitude envelope is modulated by a sinusoidal of lower frequency (fl). The following equation describes this signal:
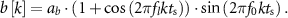
The nominal values of fn and ζ were set equal to 20 Hz and 0.092, respectively. These parameters correspond to the frequency and damping of the dominant mode in the patient evoked response model described below. Parameters ab, f0, and fl were equal to 10 µV, 20 Hz and 2 Hz, respectively. The temporal and time–frequency response to stimulation of the neural circuit's synthetic model with the above nominal parameters are depicted in figures 2(a) and (c). To understand whether the stimulation pulse sequences derived with the nominal evoked response model differed from those obtained with distinct evoked response dynamics, we characterized how deviations in ζ and fn impact the optimized stimulation sequences. Parameters ζ and fn were varied from 0.1 to 1, and from 10 to 30 Hz, respectively. The range used for the damping ratio spans the neural evoked dynamics from a lightly to a highly damped response We selected a natural frequency range that deviates +/− 50 from the spontaneous oscillations' natural frequency (f0 = 20 Hz).
from the spontaneous oscillations' natural frequency (f0 = 20 Hz).
Figure 2. Stimulation-evoked responses (ER) for the generalized and patient-specific models are presented in (a) and (b), respectively. The patient-specific model characterizes the neural response in the GPi evoked by stimulation in the GPi in a PD patient. Wavelet scalograms (time–frequency maps) of the stimulation-evoked responses for the generalized mathematical model and patient-specific model are presented in (c) and (d). Power spectral density (PSD) of spontaneous LFP activity for the generalized and patient-specific models are presented in (e) and (f).
Download figure:
Standard image High-resolution image 2.1.2. Patient-specific modelA model of both spontaneous and stimulation-evoked neural activity in the GPi of a Parkinson's disease patient was used to assess whether the results obtained with the generalized, low-order model can be applied to more complex and realistic neural dynamics. The patient-specific model was presented in a previous publication in which the input-output relationship between stimulation in the GPi and evoked responses in the GPi was estimated using instrumental variable system identification [14]. Briefly, the equations of differences describing the patient's evoked response have two imaginary pairs of poles (modes) with natural frequencies equal to 14 and 20 Hz, and corresponding damping ratios equal to 0.22 and 0.092. The frequency response of the evoked response mathematical model indicated that the largest gain in the transfer function from stimulation input to evoked response is at 19.2 Hz, near the mode with the lowest damping (f0 = 20 Hz, ζ = 0.092). It is worth mentioning that the transfer function gain does not peak where the dominant oscillatory mode is located (i.e. 20 Hz) because the 14 Hz mode is present, too. The time–frequency response of the neural dynamics evoked by stimulation are shown in figures 2(b)–(d) and a more detailed description of the model is presented in [14]. Having evoked response dynamics with their largest gain at 19.2 Hz implies that periodic stimuli at 19.2 Hz result in the largest steady state, periodic evoked responses at this frequency. Therefore, stimulation pulses can be used to modulate neural activity near 19.2 Hz with minimum amplitude.
The spontaneous neural activity used in the patient model was characterized by synthetic LFP signals that match the PSD observed in the GPi of a Parkinson's disease patient in the resting, awake state. The patient's evoked response model and PSD can be found in [14]. In this model, the spontaneous oscillations' frequency matches the resonant frequency of the stimulation-evoked responses. The synthetic LFP signal is given by
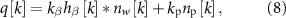
where  is the convolution operator, hβ
is a first-order Butterworth filter with a pass-band in the 17–21 Hz range, nw is zero mean Gaussian white noise with unitary power,
is the convolution operator, hβ
is a first-order Butterworth filter with a pass-band in the 17–21 Hz range, nw is zero mean Gaussian white noise with unitary power, 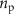 is a pink noise signal with unitary power, and
is a pink noise signal with unitary power, and  12.6 and
12.6 and 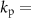 6 are constant scalars that are adjusted to match the PSD of the studied patient. The convolution between filter hβ
and the white noise nw is equal to the modeled beta band oscillations. The filter's pass-band is centered at around 19 HZ, matching closely the frequency where the stimulation-evoked response model has its largest gain (19.2 Hz). The pink noise
6 are constant scalars that are adjusted to match the PSD of the studied patient. The convolution between filter hβ
and the white noise nw is equal to the modeled beta band oscillations. The filter's pass-band is centered at around 19 HZ, matching closely the frequency where the stimulation-evoked response model has its largest gain (19.2 Hz). The pink noise 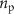 is used to characterize the
is used to characterize the 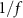 background activity observed in LFP neural recordings [3, 4].
background activity observed in LFP neural recordings [3, 4].
The signal targeted for modulation (![$b[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn28.gif) ) was obtained by filtering the synthetic LFP (
) was obtained by filtering the synthetic LFP (![$q[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn29.gif) ) in the 14–24 Hz band using a second order Butterworth filter. See the PSD of the synthetic LFP in figure 2(f).
) in the 14–24 Hz band using a second order Butterworth filter. See the PSD of the synthetic LFP in figure 2(f).
We considered stimulation sequences subject to two distinct sets of constraints in our analysis and optimization algorithms. These stimulation constraints are described below.
(i)
Stimulation pulses with adjustable amplitude: this class of stimulation sequences consists of pulses whose amplitude and timing are freely selected by the optimization. An example of a stimulation sequence with varying timing and amplitude is shown in figure 3(a) and its corresponding evoked response is shown in figure 3(b). For the mathematical formulation of our optimization problem, we employed the instantaneous normalized stimulation input![$x[k] = \frac} u[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn30.gif) as the free optimization variable. This variable can take any value in the continuous compact interval
as the free optimization variable. This variable can take any value in the continuous compact interval ![$[-1,0]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn31.gif) .
. 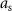 is a constant equal to the maximum allowed stimulation current. The input
is a constant equal to the maximum allowed stimulation current. The input ![$x[k] = -1$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn33.gif) corresponds to stimulation pulse with the largest allowed amplitude and
corresponds to stimulation pulse with the largest allowed amplitude and ![$x[k] = 0$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn34.gif) corresponds to the stimulation current that does not evoke a neural response. The values of the stimulation variable are negative or zero because the negative phase of the stimulation pulse (cathodal stimulation) was assumed to evoke the neural response [12].
corresponds to the stimulation current that does not evoke a neural response. The values of the stimulation variable are negative or zero because the negative phase of the stimulation pulse (cathodal stimulation) was assumed to evoke the neural response [12].(ii)
Stimulation pulses with binary amplitude values: the second class of stimulation sequences consists of pulses whose amplitude can be equal to either zero or a non-zero constant. This constraint on the stimulation pulse amplitude was studied only because present closed-loop neurostimulation systems allow us to deliver these sequences in humans [14], but not pulses whose amplitude can be adjusted in real-time. An example of a stimulation sequence with binary pulse amplitudes is shown in figure 3(c) and its corresponding evoked response is shown in figure 3(d). We used the instantaneous normalized stimulation input![$x[k] = \frac} u[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn35.gif) as the optimization variable.
as the optimization variable. ![$x[k]$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn36.gif) can take a value equal to either minus one or zero. Hence,
can take a value equal to either minus one or zero. Hence, 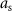 is the stimulation pulse amplitude when
is the stimulation pulse amplitude when ![$x[k] = -1$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn38.gif) .
.Figure 3. Examples of two different stimulation pulse patterns considered in this study and the corresponding evoked responses (ER) computed with the generalized, low-order model. A sequence of three pulses with adjustable amplitude and corresponding evoked response are presented in (a) and (b), respectively. A sequence of pulses with binary amplitude values and corresponding evoked responses are shown in (c) and (d).
Download figure:
Standard image High-resolution imageThe goal of the optimization is to discover stimulation pulse sequences that maximize suppression or amplification of frequency-specific neural activity given the constraints described above. The mathematical function we aim to minimize is the 2-norm of the difference between the spontaneous neural activity and a reference signal to be tracked. This cost function is given by
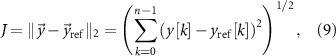
where 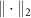 represents the 2-norm and
represents the 2-norm and 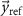 is the reference signal. The cost function J has the same unit as the LFP signal amplitude, which in our case is micro-volts (
is the reference signal. The cost function J has the same unit as the LFP signal amplitude, which in our case is micro-volts (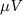 ). The reference signal is set equal to zero when we want to suppress the spontaneous oscillations (i.e.
). The reference signal is set equal to zero when we want to suppress the spontaneous oscillations (i.e. ![$\vec_\mathrm[k] = 0$](https://content.cld.iop.org/journals/1741-2552/21/3/036045/revision2/jnead54f0ieqn42.gif) for all k). When we want to amplify the targeted neural activity, we set the reference signal equal to a sinusoidal with the same frequency and phase as the spontaneous oscillations but with a larger amplitude.
for all k). When we want to amplify the targeted neural activity, we set the reference signal equal to a sinusoidal with the same frequency and phase as the spontaneous oscillations but with a larger amplitude.
We considered electrical stimulation sequences with pulses delivered at samples k (i.e. samples at times 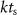 ). A sampling period
). A sampling period 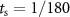 sec was used in the optimization routines to ensure that stimulation pulses were generated with a frequency smaller than or equal to the sampling frequency (
sec was used in the optimization routines to ensure that stimulation pulses were generated with a frequency smaller than or equal to the sampling frequency ( Hz). This frequency is smaller than the maximum frequency allowed in commercial DBS systems approved by the FDA for the treatment of neurological conditions [18]. This sampling frequency is also large enough to capture the neural dynamics associated with spontaneous and stimulation-evoked oscillations with a frequency below 30 Hz. To formulate the optimization problem using convex or mixed-integer tools, we represent the solution to the equations of differences (1) and (2) using a matrix multiplication:
Hz). This frequency is smaller than the maximum frequency allowed in commercial DBS systems approved by the FDA for the treatment of neurological conditions [18]. This sampling frequency is also large enough to capture the neural dynamics associated with spontaneous and stimulation-evoked oscillations with a frequency below 30 Hz. To formulate the optimization problem using convex or mixed-integer tools, we represent the solution to the equations of differences (1) and (2) using a matrix multiplication:

Vector 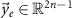 represents the evoked response samples, vector
represents the evoked response samples, vector  is the optimization pulse pattern that represents the normalized amplitude of the stimulation pulses, and
is the optimization pulse pattern that represents the normalized amplitude of the stimulation pulses, and 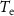 is a
is a 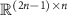 Toeplitz matrix that maps the stimulation sequences to the evoked response vector [19]. The above matrix multiplication performs the convolution between the stimulation pulse pattern and the evoked response mathematical model to obtain the evoked response time series. The combined stimulation-evoked and spontaneous neural activity represented in vector form (
Toeplitz matrix that maps the stimulation sequences to the evoked response vector [19]. The above matrix multiplication performs the convolution between the stimulation pulse pattern and the evoked response mathematical model to obtain the evoked response time series. The combined stimulation-evoked and spontaneous neural activity represented in vector form (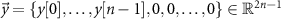 ) is given by
) is given by

Vector 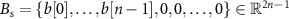 represents the zero-padded spontaneous neural activity. This vector is padded with zeros to match the dimensions of the Toeplitz matrix
represents the zero-padded spontaneous neural activity. This vector is padded with zeros to match the dimensions of the Toeplitz matrix 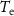 , which is
, which is 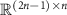 .
.
The optimization problem for stimulation pulses with adjustable amplitude is described by the expression
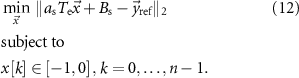
In the above optimization problem, 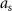 is set equal to the maximum allowed stimulation current. This optimization problem is convex. Therefore, if a solution exists, it is unique and the global minimum [20]. We denote the solution to this optimization problem as
is set equal to the maximum allowed stimulation current. This optimization problem is convex. Therefore, if a solution exists, it is unique and the global minimum [20]. We denote the solution to this optimization problem as 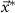 .
.
For stimulation pulses with binary amplitude values, the optimization problem is
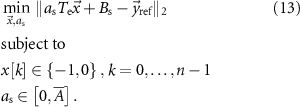
In this case, the constant scalar as becomes an optimization variable. 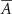 is the maximum value that
is the maximum value that 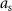 is allowed to take (i.e. maximum stimulation current). The optimal values for this optimization problem are denoted as
is allowed to take (i.e. maximum stimulation current). The optimal values for this optimization problem are denoted as 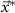 and
and 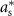 . This optimization problem is not convex. Therefore, a minimum solution, if it exists, is not guaranteed to be unique or global [20]. We used mixed-integer optimization algorithms to compute solutions to the optimization problem (13).
. This optimization problem is not convex. Therefore, a minimum solution, if it exists, is not guaranteed to be unique or global [20]. We used mixed-integer optimization algorithms to compute solutions to the optimization problem (13).
All the simulations and optimization algorithms were implemented in Matlab (MathWorks, Natick, MA, USA) and a computer equipped with an Intel Core i7-8700 K CPU processor (3.7 GHz) and a 32 GB RAM memory. For the optimization, we integrated the CVX package with Matlab [20] and solutions were obtained using the Gurobi solver. This solver was chosen because it has the capability of solving both convex and mixed-integer optimization problems [21, 22].
The optimization routines applied to both the low-order and patient-specific models were implemented with 2 s long LFP time series (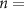 360 samples). This period was sufficient to determine the steady-state stimulation patterns needed to modulate the targeted oscillations. It also enabled us to attain a solution to the mixed-integer optimization problem with a desired gap and within a reasonable time (
360 samples). This period was sufficient to determine the steady-state stimulation patterns needed to modulate the targeted oscillations. It also enabled us to attain a solution to the mixed-integer optimization problem with a desired gap and within a reasonable time (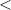 20 s). At each step, the solver internally calculates the best known objective function value for a feasible solution and the objective function lower bound. The optimal objective value is always between these two values. When the relative gap between these objective bounds is smaller than the 'MIPGap' parameter of the solver, the optimization terminates. The MIPGap was set to 0.1 for our optimization.
20 s). At each step, the solver internally calculates the best known objective function value for a feasible solution and the objective function lower bound. The optimal objective value is always between these two values. When the relative gap between these objective bounds is smaller than the 'MIPGap' parameter of the solver, the optimization terminates. The MIPGap was set to 0.1 for our optimization.
We quantified the degree of modulation achieved by pulse sequences with adjustable or binary stimulation amplitudes using the optimal value of the optimization cost function 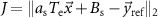 .
.
Comments (0)