Topology of surface electromyogram signals: hand gesture decoding on Riemannian manifolds

Objective. Decoding gestures from the upper limb using noninvasive surface electromyogram (sEMG) signals is of keen interest for the rehabilitation of amputees, artificial supernumerary limb augmentation, gestural control of computers, and virtual/augmented realities. We show that sEMG signals recorded across an array of sensor electrodes in multiple spatial locations around the forearm evince a rich geometric pattern of global motor unit (MU) activity that can be leveraged to distinguish different hand gestures. Approach. We demonstrate a simple technique to analyze spatial patterns of muscle MU activity within a temporal window and show that distinct gestures can be classified in both supervised and unsupervised manners. Specifically, we construct symmetric positive definite covariance matrices to represent the spatial distribution of MU activity in a time window of interest, calculated as pairwise covariance of electrical signals measured across different electrodes. Main results. This allows us to understand and manipulate multivariate sEMG timeseries on a more natural subspace—the Riemannian manifold. Furthermore, it directly addresses signal variability across individuals and sessions, which remains a major challenge in the field. sEMG signals measured at a single electrode lack contextual information such as how various anatomical and physiological factors influence the signals and how their combined effect alters the evident interaction among neighboring muscles. Significance. As we show here, analyzing spatial patterns using covariance matrices on Riemannian manifolds allows us to robustly model complex interactions across spatially distributed MUs and provides a flexible and transparent framework to quantify differences in sEMG signals across individuals. The proposed method is novel in the study of sEMG signals and its performance exceeds the current benchmarks while being computationally efficient.

sEMG signals are recorded non-invasively by placing sensors on the skin surface and measuring electrical signals arising from motor unit (MU) activation. Global characteristics of the sEMG signal such as its amplitude and power spectrum depend on numerous idiosyncratic factors: anatomical characteristics including thickness of the subcutaneous tissue, distribution and size of MU territories, and spread of endplates and tendon junctions within the MU; physiological factors such as distribution of conduction velocities of the fibers within the MUs, shape of intracellular action potentials [5], and muscle fatigue [4]; and circumstantial factors such as the precise electrode placement [9, 12]. The combined effect of these factors is further complicated by the interactions of signals originating from multiple, neighboring muscles. Consequently, signals from individual sEMG electrodes tend to be highly confounded and opaque, thereby limiting their practical use. We show that covariance matrices constructed using pairwise covariance of electrical signals measured across different electrodes capture the combined effect of various physiological and anatomical factors and provide a framework to quantify the differences in sEMG signals across individuals. Moreover, the spatial signal patterns captured by covariance matrices showcase rich geometric patterns that can be used to distinguish distinct hand gestures.

Existing methods use constructed features such as signal root-mean-square, time domain statistics as described by Hudgins et al [8], histograms [28], marginalized discrete wavelet transform [16], or the normalized combination of all of the above. These features are often evaluated with classifiers such as linear discriminant analysis (LDA), support vector machines, k-nearest neighbors (k-NN), and random forests. Additionally, some works use deep learning models such as convolutional neural networks (CNN) [6, 11, 22, 25], recurrent neural networks (RNN) [19, 23], transformer-based networks [18, 20], and networks constructed by combining RNN and CNN [7, 21]. Xiong et al [26] analyze sEMG signals using symmetric positive definite (SPD) covariance matrices; however, by mapping the learned features on the manifold onto a tangent plane and by decoding them in the Euclidean space, this approach does not leverage the advantages of the natural geometrical structure of the data. All of the above methods fail to account for strong spatial correlations in the muscle contraction patterns. Additionally, these approaches may have a large number of training parameters, in the range of tens of thousands, and tend to require complex transfer learning paradigms and retraining while deploying across individuals. None of the established techniques easily adapt to signal changes due to factors such as muscle fatigue and deviations in sensor positions.

We demonstrate that analysis of sEMG signals on a Riemannian manifold is more comprehensive and naturally suited for the data structure than the usual analysis in Euclidean space. SPD covariance matrices constructed from the multivariate sEMG timeseries lie on a cone manifold equipped with a Riemannian metric. For computational efficiency and numerical stability, we study the SPD matrices via Cholesky decomposition in the Cholesky space [15], the collection of lower triangular matrices whose diagonal elements are all positive. We demonstrate that covariance matrices from different individuals lie in different neighborhoods of the manifold space owing to the combined influence of an individual's anatomical and physiological factors on the sEMG signals and that the difference in sEMG signals among individuals can be quantified using the geodesic distance (length of the shortest curve between two points on a surface) between corresponding covariance matrices. We present two supervised learning algorithms (manifold minimum distance to mean (MDM) and manifold support vector machine (SVM)) and one unsupervised learning algorithm (manifold k-medoids clustering) to classify hand gestures on the Riemannian manifold.

We describe below the principles of using SPD covariance matrices, the means of operating on the Riemannian Manifold, and the distance metrics with which we characterize variability, e.g. across individual subjects and distinct gestures.

2.1. Definitions

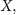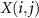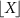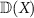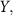For a square matrix $X,$ whose dimension is c, $X(i, j)$ denotes its element in the ith row and jth column. $\lfloor X\rfloor$ denotes a c × c matrix whose (i, j) element is Xij if i > j and is zero otherwise. $\mathbb(X)$ denotes a c × c diagonal matrix whose (i, i) element is Xii . For two square matrices X and $Y,$ Frobenius inner product 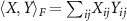$\langle X, Y\rangle_F = \sum_^X_Y_$ and the induced Frobenius norm is 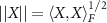$||X|| = \langle X, X\rangle_F^$. For X, a lower triangular matrix 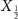$X_}$ is defined as 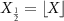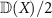$X_} = \lfloor X\rfloor$ + $\mathbb(X)/2$. The matrix exponential map of a real matrix is defined by 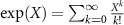$\exp(X) = \sum_^\frac$ and its inverse, the matrix logarithm, whenever it exists and is real, is denoted by 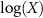$\log(X)$. It is noted that the matrix exponential and logarithm of a diagonal matrix is also a diagonal matrix. Mathematical formulation and notations used here are borrowed from Lin [15].

2.2. Operating on the manifold of SPD matrices

SPD matrices of dimension c, denoted by 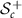$\mathcal_c^+$, is a convex smooth submanifold of the space 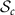$\mathcal_c$ of symmetric matrices with the Euclidean space 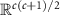$\mathbb^$. For a matrix 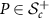$P\in\mathcal_c^+$, Cholesky decomposition expresses P as a product of lower triangular matrix L and its transpose; that is, 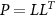$P = LL^T$. If the diagonal elements of L are restricted to be positive, Cholesky decomposition is unique [15]. Lower triangular matrices of dimension c whose diagonal elements are all positive, denoted by 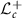$\mathcal_c^+$, is a smooth submanifold of the space 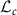$\mathcal_c$ of lower triangular matrices with the Euclidean space 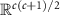$\mathbb^$. Cholesky decomposition denoted by 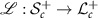$\mathscr:\mathcal_c^+\rightarrow\mathcal_c^+$ is bijective, that is, there is a one-to-one correspondence between SPD matrices and lower triangular matrices whose diagonal elements are all positive [15]. The inverse map is denoted by 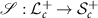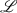$\mathscr:\mathcal_c^+\rightarrow\mathcal_c^+$. $\mathscr$ and its inverse 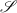$\mathscr$ are diffeomorphisms, that is, differentiable map 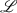$\mathscr$ is a bijection and its inverse 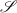$\mathscr$ is differentiable as well. Space 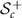$\mathcal_c^+$ is the Riemannian space and the space 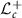$\mathcal_c^+$ is the Cholesky space.

2.3. Riemannian metrics

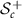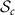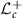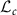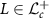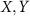Tangent space at a given matrix in $\mathcal_c^+$ is identified with $\mathcal_c$. Tangent space at a given matrix in $\mathcal_c^+$ is identified with $\mathcal_c$. For $L\in \mathcal_c^+$ and $X, Y$ in the tangent space at L denoted by 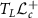$T_L\mathcal_c^+$ (identified with 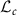$\mathcal_c$), Riemannian metric 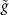$\tilde$ for tangent space is given by

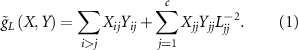
Equation (1)

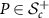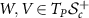Riemannian metric g for $P\in\mathcal_c^+$ and $W, V \in T_P\mathcal_c^+$ (identified with 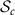$\mathcal_c$) is given by

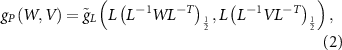
Equation (2)

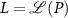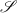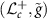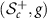where $L = \mathscr(P)$. The map $\mathscr$ is an isometry between $(\mathcal_c^+, \tilde)$ and $(\mathcal_c^+, g)$ [15]. A Riemannian isometry provides correspondence of Riemannian properties and objects between two Riemannian manifolds. This enables us to study the properties of 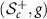$(\mathcal_c^+, g)$ via the manifold 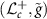$(\mathcal_c^+, \tilde)$ and the isometry 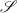$\mathscr$. The metrics presented here are computationally efficient and numerically stable compared to affine-invariant and Log-Euclidean metrics (directly operating with SPD matrices using affine-invariant Riemannian metric involves computing matrix logarithm and exponential which involve evaluating a series of infinite terms [1]). Specifically, under this construction, Fréchet mean and parallel transport are given in a closed form and we can construct a positive definite kernel for SVM (which is not possible with the affine-invariant metric [10]).

2.3.1. Geodesic distance metric

For any two points L, K in 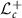$\mathcal_c^+$, we have a unique geodesic curve (shortest path between two points) connecting L and K. The arc length of the geodesic curve, that is, the geodesic distance in 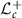$\mathcal_c^+$ between L and K is given by

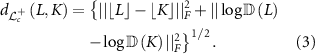Equation (3)2.3.2. Average of finite SPD matrices

For 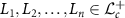$L_1, L_2, \ldots, L_n\in\mathcal_c^+$, the Fréchet average is

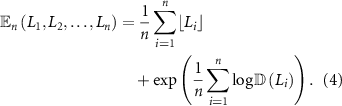Equation (4)2.4. MDM algorithm

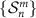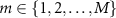Given M classification classes and N training samples, SPD matrices in the training set $\_n^m\}$, where $n\in\$ and $m\in\$ are used to construct centroids for each of the M classes such that the centroid of class m is,

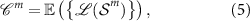
Equation (5)

where the Fréchet mean is calculated according to equation (4). Given a test dataset of SPD matrices 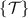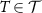$\\}$, $T\in\mathcal$ is assigned to that class whose centroid is nearest to 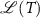$\mathscr(T)$. That is, the class of T is

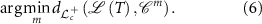Equation (6)2.5.  k-Medoids algorithm

We implement the classic k-medoids algorithm using partitioning around medoids heuristic by replacing the Euclidean distance with the distance in equation (3).

2.6. SVM

For training the SVM, we use a kernel 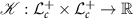$\mathscr: \mathcal_c^+ \times \mathcal_c^+\rightarrow \mathbb$, such that

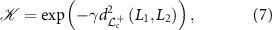
Equation (7)

where L1, 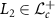$L_2\in \mathcal_c^+$ and γ > 0. In appendix A, following the arguments in Jayasumana et al [10], we prove that the kernel in equation (7) is a valid kernel.

We use three data sets in this study. The first (Ninapro) is publicly available from Atzori et al [2], the second (high density sEMG signals) is publicly available from Malešević et al [17], and the third (UCD-MyoVerse-Hand-0) was collected and curated by us at the University of California, Davis.

3.1. Dataset 1 - Ninapro

We choose the widely used Ninapro (Non-Invasive Adaptive Prosthetics) Database 2-Exercise 1 [2] to test our algorithms and to compare them against the existing benchmarks. The dataset consists of sEMG signals obtained from forty intact subjects using twelve electrodes. Eight electrodes were placed equally spaced around the forearm at the height of the radio-humeral joint; two electrodes were placed on the main activity spots of the flexor digitorum superficialis and of the extensor digitorum superficialis. Subjects performed seventeen different gestures, each repeated six times. The seventeen gestures are: thumb up, extension of index and middle—flexion of the others, flexion of ring and little finger—extension of the others, thumb opposing base of little finger, abduction of all fingers, fingers flexed together in fist, pointing index, adduction of extended fingers, wrist supination (axis: middle finger), wrist pronation (axis: middle finger), wrist supination (axis: little finger), wrist pronation (axis: little finger), wrist flexion, wrist extension, wrist radial deviation, wrist ulnar deviation, and wrist extension with closed hand. See Atzori et al [2] for further details on data acquisition and processing.

3.2. Dataset 2 - high density sEMG signals from Malešević et al [17]

The dataset consists of sEMG signals obtained from nineteen intact subjects using 128 electrodes recorded at the level of the forearm. (The experiment included twenty intact subjects, however the data corresponding to Subject 5 is corrupted.) Subjects performed 65 unique gestures that are combinations of 16 basic single degree of freedom movements. Each gesture was repeated five times. See Malešević et al [17] for further details on data acquisition and processing.

3.3. Dataset 3 - UCD-MyoVerse-Hand-0

A total of thirty subjects (age range: 18–76 years) participated in our study. Forearm sEMG was collected from intact subjects using twelve electrodes. Eight electrodes were placed equally spaced around the main belly of the forearm muscles below the elbow at approximately 1/3 the distance from elbow to wrist. Four electrodes were placed equally spaced around the wrist joint. Each subject performed ten different hand gestures, with each gesture performed thirty-six times. The ten gestures are: wrist movement in four cardinal directions (up, down, left, and right), three pinches (index finger pinch, middle finger pinch, two-finger pinch), splay, power grasp, and pointing index (figure 1). The 10 gestures were chosen to reflect the commonly used gestures for interacting with computers. Hand gestures in cardinal directions can be used to move the screen up, down, left, and right. The pinches can be used for zoom-in, zoom-out, and selections.

Figure 1. Ten gestures included in the UCD-MyoVerse-Hand-0 experiment. From top-left: up, down, left, right, index point, two finger pinch, power grasp, middle finger pinch, splay, index finger pinch.

Download figure:

Standard image High-resolution image 3.3.1. Data acquisition protocol

For Dataset 3, we use Delsys double differential sEMG electrodes (Delsys, Inc) and NI USB-6210 multifunction I/O (National Instruments Corporation — 16-inputs, 16-bit, 250kS/s) data acquisition system for acquiring sEMG data at a rate of 2000 Hertz. Delsys electrodes transmitted the acquired data via a wireless network to the base station. Data from the base station was relayed to the computer via a USB connection through the NI USB-6210 data acquisition system. A graphical user interface (GUI) was designed to display hand gestures on a screen. Subjects performed the displayed gesture with their dominant hand while comfortably seated in a chair with the forearm resting on an elevated platform on the table (subjects were allowed to choose a resting position that they were most comfortable with. They were also allowed to change the resting position throughout the experiment). Each gesture lasted for 2 s followed by a resting period of 2 s. (The gesture was displayed on the screen for a period of 2 s followed by a blank screen for a period of 2 s; subjects were instructed to perform the gesture for the duration the image was present on the screen and rest during the blank screen.) The experiment was divided into six sessions (figure 2). Each session consisted of sixty trials: six repetitions for each of the ten gestures. The order of gestures within a session was pseudorandomly generated. This was done to assess how variations in making gestures affect the decoding accuracy (if all 6 repetitions for a gesture occurred sequentially, it would encourage repetitive and almost unconscious and extremely consistent movements). In total, each subject completed 360 trials.

Figure 2. Our experiment has 6 sessions. Data from the first 3 sessions are used for training supervised models. Data from the last 3 sessions are used for testing the supervised models. Each session has 60 trails - 10 distinct gestures, each repeated 6 times. In total, we have 360 trials per individual subject.

Download figure:

Standard image High-resolution image

We used ZeroMQ sockets (https://zeromq.org/socket-api/) and Lab Streaming Layer (https://github.com/sccn/labstreaminglayer) in Python to time sync GUI instructions with data streamed from the Delsys system. Data streams were synced to the master clock on the computer that received both sEMG data and event markers from the GUI. We observed a maximum clock drift of around 50 ms.

4.1. Dataset 14.1.1. Preprocessing

In Dataset 1, sEMG data was collected at a frequency of 2000 Hz using 12 electrodes. Each gesture was 5 s long followed by a 3 s resting position. We use Database B - Exercise 1 with 17 hand gestures. For a detailed description, refer to Atzori et al [2]. For each gesture, sEMG data is a matrix X which has 10 000 columns (temporal dimension - 5 s × 2000 Hz) and 12 rows (12 electrode channels). Therefore, the dimensions of X are 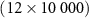$(12\times 10\,\,000)$. We normalize the data along the time dimension for every channel. We construct a sample covariance SPD matrix $P = \fracXX^T$. P has dimensions 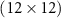$(12\times 12)$. Therefore, the SPD matrices are represented in 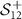$\mathcal_^+$ (space of SPD matrices whose dimensions are 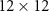$12 \times 12$). We use MDM, SVM, and k-medoids algorithms as explained previously to classify the SPD matrices in 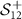$\mathcal_^+$. We compare the results obtained with our methods to results obtained in Sun et al [23] and Rahimian et al [20] (table 1). We provide the results for all 40 subjects using manifold methods in table 2.

Table 1. Our proposed methods perform better by leveraging manifold representation. The proposed unsupervised k-medoids algorithm, to the best of our knowledge, is the only unsupervised algorithm for sEMG signal classification. Unlike other methods which have neural networks with tens of thousands of parameters, our algorithms are computationally efficient.

 MethodAccuracy 4-layer 3rd order dilation0.824 4-layer 3rd order dilation (pure LSTM)0.797 4-layer 2nd order dilation (pure LSTM)0.796 4-layer 1st order dilation (pure LSTM)0.793Sun et al [23]4-layer baseline0.753 2-layer CNN0.746 2-layer LSTM0.702 1-layer LSTM0.684 2-layer MLP0.662 SVM (Euclidean)0.307 TEMGNet 200 ms window0.821Rahimian et al [20]TEMGNet 300 ms window0.829 Manifold MDM0.92Proposed manifoldManifold SVM0.93methodsManifold k-medoids0.82

Table 2. Classification accuracy for 40 subjects in Dataset 1. Following the works in Sun et al [23] and Rahimian et al [20], for each gesture, we use repetitions 1, 3, 4, and 6 for training and repetitions 2 and 5 for testing of MDM and SVM algorithms.

 Classification methodsSubject numberMDMSVM (γ = 8) k-medoids01.01.00.9010.940.970.8620.970.970.7830.940.940.7940.971.00.8550.850.850.7960.880.880.697
View original article
JOURNAL OF NEURAL ENGINEERING

Comments (0)

No login
gif
format_indent_decrease