Neuromorphic circuits are fundamental building blocks for brain-inspired computing tasks in artificial intelligence applications [1]. Several such neuronal hardware models are reported in [2–9]. However, the complex electrophysiological properties of a biological neuron, such as post-inhibitory rebound excitation (PIRE), are not discussed in the above mentioned works. Integrating PIRE in neuromorphic circuits is crucial because it leads to persistent or self-sustained neural activity [10]. Persistent activity is an important element in cognitive and developmental systems supporting functions such as working memory, decision-making, and attention [11]. Neuromorphic circuits with persistence phenomenon can potentially enhance our understanding of neural processing and create more energy-efficient, brain-like computing systems [12].

Neuronal communication occurs through action potentials. Membrane potential (typical range −70 mV to +40 mV) of a neuron rises upon receiving excitatory inputs [13]. This leads to a spike (amplitude ≈80 mV, duration ≈2 ms) when it surpasses the threshold (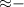40 mV). In response to the inhibitory input current pulse, the membrane potential decreases from its resting potential (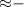70 mV) [14]. A spike can also occur following the cessation of a potent, long-lasting hyperpolarizing input [15]. This extended hyperpolarization leads to a drop in the membrane potential and spiking threshold. When this input is terminated, the membrane potential rapidly increases and becomes suprathreshold. Hodgkin and Huxley first modeled this event and named it anode break excitation [15], which, however, is also known as PIRE [16].

Research in spiking neurons has recently gained significant attention due to spiking neuron's remarkable cognitive abilities and low energy consumption. Several computational models of a spiking neuron are developed, viz. Hodgkin–Huxley [15], various leaky integrate and fire (LIF) models [17], Izhikevich and spike response model (SRM) [18]. Furthermore, researchers have designed hardware models to emulate the electrophysiological properties of a neuron. The authors in [3, 4, 7, 8] have generated different patterns of spiking, such as fast, regular, bursting, and chattering using neuromorphic circuits. However, unlike a biological neuron, the resting potential is reported to be around 0 V. Chen et al have used a small number of transistors to design a neuron in CMOS but the spike amplitude (≈500 mV) largely differed from a biological neuron [9].

Several CMOS synaptic (connections between two neurons) circuits are presented in [6, 19] and [20]. These models convert a presynaptic voltage obtained from a source neuron into a postsynaptic current injected to a target neuron [19]. Synapses are also designed with memristors (a non-linear passive electronic memory element) in hardware [21, 22]. Memristors offer a promising advantage in synaptic circuits by emulating the dynamic plasticity of biological synapses, enabling energy-efficient learning and memory functions in artificial neural networks. Their ability to store and modulate resistance values allows for fine-tuning of synaptic weights, mimicking the brain's synaptic plasticity. However, CMOS technology has been developed and optimized for decades, making it highly reliable, readily available, and cost-effective for a wide range of integrated circuits.

The above survey shows that researchers have attempted to capture different electrophysiological properties of a biological neuron. However, the parameters obtained are not in accordance with a biological neuron. Only the Hodgkin and Huxley model can incorporate PIRE in a computational model of a spiking neuron. Although the Hodgkin and Huxley model has been designed using NMOS and BJTs, presented in [23, 24] respectively, the PIRE mechanism has not been included. PIRE has been described in hardware using the negative resistance property of CMOS circuits [25]. An application has been shown where the CMOS neuron behaves as a neural oscillator. However, the simulation results shown in [25] are not bio-plausible such as the spike amplitude (3 V) and duration (100 us) reported, do not match the biological range. In [26], PIRE has been discussed using a hardware neuronal network for the auditory detection feature circuits of crickets, where the excitatory input is delayed by long inhibitory input causing the post-inhibitory rebound phenomenon. However, no spike has been generated during PIRE as the amplitude of around 0.1 mV is shown whereas the membrane potential range reported in [26] is around 0 to 1.2 V, which is not similar to that of biological neuron's range.

PIRE is a commonly observed phenomenon in the human brain [27–30]. PIRE also plays an important role in the development of oscillations in the brain, maintains self-sustaining spiking activity [10], crucial in producing offset responses of sound [31] and on-off responses in the visual receptive field [32]. Moreover, as a 'memory mechanism,' inhibitory rebound that develops and fades over many seconds enables a neuron to remember the history of inhibitory inputs for a long time. This is termed as persistent activity or self-sustaining neuronal spiking activity [10] and plays a crucial role in working memory, a key component of attention [33] and decision-making [34] which is observed in the prefrontal cortex of the brain. In this work, the PIRE mechanism has been incorporated into an individual neuron. Then, we use such models with PIRE by including a handful of neurons that exhibit persistent activity.

The key contributions of this paper are as follows.

This study introduces a novel method for incorporating the PIRE phenomenon, adding a significant element of realism and functionality to the hardware neuron. Incorporating PIRE into a hardware spiking neuron is important as it can potentially elevate neuromorphic circuits' overall bio-plausibility and cognitive capacity, aligning them more closely with biological counterparts.The developed neuromorphic circuit with PIRE generates persistent activity with the help of two spiking neuronal networks. Persistent activity or self-sustaining activity is associated with various cognitive functions resembling working memory, attention, and decision-making.

The remainder of the paper is organized as follows. The method followed to design the PIRE-integrated neuron and synaptic circuits is discussed in section 2. The responses obtained from the circuits presented in section 2 are shown in section 3. Section 4 gives the comparison of the proposed neuronal circuit with other hardware neuron models. Further, this section discusses the implications of persistent activity in neuromorphic circuits. Finally, section 5 gives the overall conclusion of the work.

In this section, the working principle of the proposed neuromorphic circuit has been discussed. Further, excitatory and inhibitory synapses that connect the PIRE-integrated neuronal circuits to form a network have been presented. Two spiking neuronal networks that generate persistent activity are discussed in the third subsection.

2.1. CMOS spiking neuron with PIRE

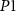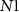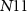The CMOS neuron is designed using 6 PMOS (—), 11 NMOS (—) transistors, 4 capacitors (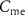, C1, C2, C3), and 16 independent voltage sources as shown in figure 1. All the simulations are done in Cadence Virtuoso using TSMC 180 nm technology, where the transistors are operated in a subthreshold region. 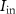is the input current stimulus of the neuronal circuit, and the membrane potential 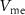gives the output.

Figure 1. Schematic of PIRE-integrated neuronal circuit.

Download figure:

Standard image High-resolution image

The operating mechanism of the neuronal circuit is discussed below using three blocks.

(a) Regular spiking block: This block controls the depolarization, repolarization, and hyperpolarization phase of a neuron. In the absence of any input, 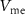is at its resting potential controlled by 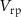[35]. 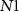acts as a leakage source, controlled by voltage 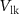with drain current 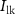. With the increase in current through 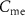(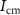), 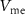increases.

Since the transistors are operated in the subthreshold region [2], so 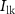is given by

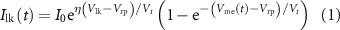
where I0 is the leakage current [2], η is the subthreshold slope factor, and Vt is the thermal voltage.

The source voltage of (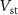) controls the spiking threshold. When 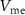crosses the threshold, charging current (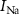) increases very rapidly by current mirror topology. This increases 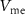within a short time and reaches the overshoot value of a spike. 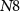is connected in series with transistor 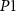to control the amplitude of spikes by voltage 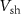. This is the depolarization phase of a neuron. The inverter's (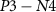) output is fed to a source voltage of 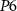. With the increase in this voltage, C1 starts to integrate, whereby increasing discharging current (IK). The gate voltage (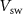) of 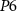(drain current Is) controls the duration of the spikes. A decrease in 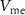occurs due to an increase in IK and a decrease in 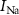. This phase is termed repolarization. With an increase in IK, 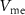decreases below the resting potential and is restored to its resting position. This is the hyperpolarization phase. During this phase, a new spike cannot occur for some time termed the refractory period, controlled by 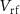(gate voltage of 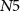), discharging C1. Since the capacitor C1 is charged and discharged by transistors 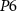and 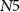respectively, so the spike duration is effectively controlled by 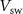and 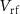. The entire process will generate regular spiking trains till an input stimulus exists.

(b) Spike frequency adaptation block: This block controls the time interval between two consecutive spikes, termed the inter-spike interval (ISI). With an increase in the number of spikes, ISI decreases [35]. The output of the inverter (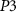-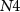) is fed to the source of 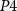(with drain current 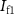) where the gate voltage of 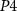(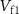) controls the charging of C2. The discharge of C2 is controlled by gate voltage (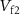) of NMOS transistor 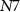(with drain current ).

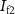(c) PIRE block: When a hyperpolarizing current is applied, 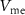decreases below its resting potential. When 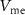is low enough, PMOS transistor 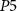(with drain current Iv) starts to conduct and charges the capacitor C3. When the capacitor C3 is sufficiently charged, current through NMOS transistor 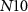increases. At the termination of a strong hyperpolarizing current, current through 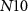(Ib) becomes sufficiently positive enough to give rise to an action potential, causing the PIRE phenomenon. The rate of discharge of the capacitor C3 is controlled by the gate voltage (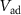) of transistor 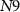(with drain current 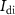), and the rise time of 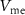(when hyperpolarized) is controlled by the gate voltage (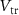) of transistor 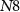(with drain current 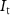). The membrane potential (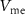) is given by

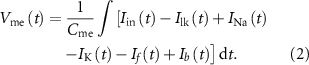2.2. Synaptic connections of neurons with PIRE

Two neurons are connected by synapses [19]. In this subsection, circuits are designed to mimic two biological synapses, viz. excitatory and inhibitory. Input to the synapse is 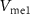, which is the output voltage of the first neuron. Output from the synapse is the postsynaptic current (PSC). This current is fed to a second neuron generating postsynaptic potentials (PSPs) at the output (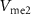). Both the excitatory and inhibitory synaptic circuits are discussed below.

2.2.1. Excitatory synaptic circuit

The schematic of the excitatory synapse is almost similar to the differential pair integrator synapse discussed in [19], except that a double inverter (as a buffer) is used after 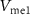to increase the strength of the presynaptic spikes.

The working principle of the schematic shown in figure 2 is discussed below.

Figure 2. Excitatory synaptic circuit between two neurons.

Download figure:

Standard image High-resolution image

Input to Neuron 1 is a current pulse 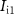, and the output of this neuron is the input to the artificial synapse in the form of membrane potential 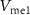. The gate voltage of 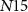(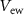) controls the synaptic weight of the excitatory synapse. Depending upon the gate voltage of 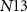(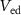), drain current of 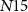will be distributed between the transistors 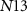and 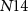. In the presence of a spike, current flowing through transistor 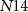(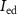) will discharge the capacitor 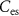. When transistor 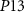(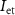) starts to conduct, it will charge 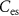. The gate voltage of 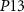(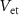) controls the time duration of PSPs. Current through 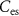is given by

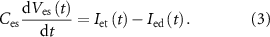
Current (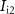) through the PMOS transistor 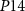is the excitatory postsynaptic current (EPSC), which is fed to the second neuron (Neuron 2) and thus generates the excitatory postsynaptic potentials (EPSPs) at the output of the second neuron (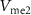). 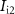is given by ( [19])

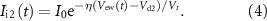
where Vt is the thermal voltage.

2.2.2. Inhibitory synaptic circuit

The inhibitory synaptic circuit shown in figure 3 follows almost the same procedure as the excitatory one with the following modifications as summarized below.

Figure 3. Inhibitory synaptic circuit between two neurons.

Download figure:

Standard image High-resolution image

All PMOS transistors of the excitatory synaptic circuit are replaced by NMOS and vice-versa in the inhibitory synapse. 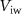(gate voltage of 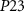) and 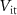(gate voltage of 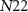) control the synaptic weight and time duration of inhibitory PSPs (IPSPs), respectively. Current through the capacitor 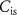is given by

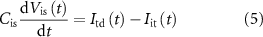
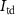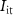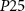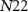where and are the drain currents of transistor and respectively.

Two neuronal networks are designed with the help of several CMOS neurons (figure 1) and synaptic (figures 2 and 3) circuits, as discussed in the next subsection. These networks are employed to demonstrate the significance of incorporating the PIRE block in neuromorphic circuits to exhibit persistent activity [