Objective. Bioimpedance spectroscopy (BIS) is a popular technique for the assessment of body composition in children and adults but has not found extensive use in babies and infants. This due primarily to technical difficulties of measurement in these groups. Although improvements in data modelling have, in part, mitigated this issue, the problem continues to yield unacceptably high rates of poor quality data. This study investigated an alternative data modelling procedure obviating issues associated with BIS measurements in babies and infants. Approach. BIS data are conventionally analysed according to the Cole model describing the impedance response of body tissues to an applied AC current. This approach is susceptible to errors due to capacitive leakage errors of measurement at high frequency. The alternative is to model BIS data based on the resistance–frequency spectrum rather than the reactance-resistance Cole model thereby avoiding capacitive error impacts upon reactance measurements. Main results. The resistance–frequency approach allowed analysis of 100% of data files obtained from BIS measurements in 72 babies compared to 87% successful analyses with the Cole model. Resistance–frequency modelling error (percentage standard error of the estimate) was half that of the Cole method. Estimated resistances at zero and infinite frequency were used to predict body composition. Resistance-based prediction of fat-free mass (FFM) exhibited a 30% improvement in the two-standard deviation limits of agreement with reference FFM measured by air displacement plethysmography when compared to Cole model-based predictions. Significance. This study has demonstrated improvement in the analysis of BIS data based on the resistance frequency response rather than conventional Cole modelling. This approach is recommended for use where BIS data are compromised by high frequency capacitive leakage errors such as those obtained in babies and infants.

Bioelectrical impedance analysis (BIA) is a commonly used method for the assessment of body composition (Moonen and Van Zanten 2021, Sbrignadello et al 2022, Branco et al 2023). Despite this popularity, BIA has not found wide use in paediatric settings (Andrews et al 2019, Lyons-reid et al 2020, Lyons-Reid et al 2021, Orsso et al 2022, Zamberlan et al 2023). In part this is due to the practical difficulties associated with performing BIA measurements in babies and infants, for example, avoiding movement artefacts during measurement, and lack of standardisation of measurement protocols (Collins et al 2013, Lingwood 2013, Brantlov et al 2017a, 2017b, Orsso et al 2022). In addition, impedance measurements in babies seem particularly prone to artefacts of measurement (Gridneva et al 2016), notably the so-called 'hook effect' due to stray and parasitic capacitances in bioimpedance spectroscopy (BIS) (Scharfetter et al 1998, Buendía et al 2010b, William et al 2022).

In contrast to single frequency BIA (SFBIA) that performs measurement of impedance (Z) at a single frequency of 50 kHz, BIS measures Z and its components, resistance (R) and reactance (Xc), over a range of frequencies, typically from 5 to 1000 kHz (Matthie 2008). Resistance and reactance data are applied to the Cole model for body fluid distribution in which the extrapolate resistance at zero frequency (R0) is proportional to extracellular water volume (ECW) while resistance at infinite frequency (R∞ ) is proportional to total body water (TBW) (Cornish et al 1993, Matthie 2008). In BIS, TBW and ECW are calculated from R0 and R∞ along with anthropometric parameters (weight, height and body proportions), body density and tissue water resistivities using mixture theory (Ward et al 2015). Unfortunately, the hook effect particularly compromises impedance measurements at high frequencies (> ∼500 kHz) markedly affecting accurate estimation of R∞ (Buendía et al 2010b). Various methods have been tried to correct for the hook effect, the most common being time delay (Td) compensation (De Lorenzo et al 1997, Scharfetter et al 1998) although this provides for only partial improvement (Buendia et al 2010a, 2010b). Since the hook effect mostly affects the phase and reactance of the complex impedance only slightly modifying the resistance–frequency spectrum, the possibility of estimating R0 and R∞ from the resistance–frequency data exists (Ayllon et al 2009). This approach has been used successfully previously in other settings (Cornish and Ward 1998, Ward et al 2020).

The aim of the present study was to compare the conventional Cole model and the resistance–frequency model for estimating R0 and R∞ in BIS measurements in neonates. In addition, body composition predicted using mixture theory based on R0 and R∞ obtained by either method was compared with body composition measured by the reference method of air displacement plethysmography (ADP).

2.1. Participants

Participants were 72 newborns randomly selected from the large prospective epidemiological 'Araraquara Cohort Study' study (Dejani et al 2023). Babies were drawn from those enrolled in the study from the Municipal Maternity Hospital in Araraquara city, São Paulo, Brazil. The study was approved by the Ethics Committee of the University of São Paulo and written consent was obtained from parents before any data collection. Gestational age was obtained from medical records.

2.2. Anthropometric measurements

Heel to crown length and weight were obtained at time of BIS and ADP measurements at an average of 7.8 weeks post-birth. Length was measured using a Seca® 416 infantometer (Seca®, Hamburg, Germany) to the nearest 0.1 cm. Weight was obtained using the Pea Pod® equipment (Cosmed®, Concord, CA, USA) to the nearest 0.1 kg.

2.3. Bioimpedance spectroscopy

Whole body (wrist to ankle) impedance measurements were obtained using a Bodystat 5000 BIS spectrometer (Bodystat Ltd, Isle of Man). Electrodes were placed at the conventional sites used in adults and children: current drive electrodes at the base of the toes and the fingers and voltage sense electrodes along the midlines between the malleoli at the ankle and bony prominences at the wrist. Electrode sites were cleaned with alcohol wipes prior to attachment of Ag-AgCl gel electrodes (Bodystat 0515). Measurement was performed within a hospital setting with babies lying electrically isolated on a non-conductive mattress. Attention was paid to avoid as far as possible extraneous electrical noise and it was ensured that measurement leads were uncoiled to minimise potential for stray capacitance errors. In order to minimise movement artefacts, data recording was commenced only when the baby was visibly quiet, i.e. not moving or crying.

2.4. Air displacement plethysmography

Body composition according to a two-compartment model (fat-free mass (FFM) and fat mass (FM)) was measured by ADP using a Pea Pod® (Cosmed, Concord, CA, USA) according to manufacturer's instructions as reported previously (Dejani et al 2023).

2.5. Data analysis

The BIS device provides Z, R, Xc and phase angle (PhA) at each of 50 logarithmically-spaced frequencies in the range, 5–1000 kHz. R and Xc were extracted and fitted to the Cole model using software based on the fitting procedure described by Cornish et al (1993) using Bioimp v4.12.0 (ImpediMed Ltd, Brisbane, Australia). Data were analysed using default settings in which data for frequencies up to 500 kHz (n = 44 frequencies) were fitted to the Cole model, graphically represented as a semi-circular Xc-R plot, with application of Td compensation for high frequency deviation. Goodness of fit was assessed visually and by the percentage standard error of the estimate (%SEE). R0 and R∞ were provided by the software from extrapolation of the fitted Xc-R curve.

R0 and R∞ were independently determined from fitting the R-frequency data. Resistance declines exponentially with frequency and the best-fitting curve was determined using nonlinear regression using the curve-fitting module of Slidewrite (7.01, Advanced Graphics Software Inc., Rancho Santa Fe, USA) as described previously (Ward et al 2020). The best fitting equation was

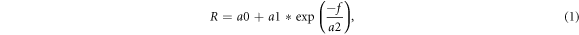
where R = resistance (ohm), f = frequency (kHz) and a0–2 are the fit coefficients. Goodness of fit was assessed by %SEE. Identical results were also obtained when curve fitting was undertaken using the Solver function of Excel or by nonlinear curve fitting using FindCurves (http://findcurves.com/ last accessed 5th December 2023). R0 and R∞ were calculated from equation (1) for zero and infinite frequency respectively. Intracellular resistance (Ri ) was calculated from R0 and R∞ :

Body composition was calculated from R0 and R∞ and calculated Ri values according to mixture theory using BatchBCA (v1.1.0 ImpediMed Ltd, Brisbane, Australia). FFM density was assumed to be 1.065 as used in ADP and body hydration fraction of 0.80 based on the data of Fomon et al (1982). Body proportion factor (kb) was calculated for each child based on height, weight and sex according to the method of Ward et al (2022). Age-appropriate apparent resistivity values were drawn from a database maintained by author Ward and were similar to those used previously (Lingwood et al 2012, Collins et al 2013, Tint et al 2016): ECW resistivity (rhoe), 960 ohm.cm and 1159 ohm.cm female and male respectively; ICW resistivity (rhoi), 1790 ohm.cm and 2202 ohm.cm female and male respectively. These are apparent resistivity coefficients whose magnitude is dependent upon their method of derivation (Ward et al 2015). There are currently no resistivity coefficients that have been derived using resistance values (R0 and R∞ ) derived from resistance–frequency curve fitting; present values having been derived using Cole modelling only. Consequently, R0 and R∞ values for participants derived from resistance–frequency modelling were converted to their Cole model equivalents using regression equations of R0 and R∞ describing the relationship between the two model values (supplementary data figures 1(A) and (B)).

Figure 1. Example BIS data as cole and resistance–frequency plots.

Download figure:

Standard image High-resolution image 2.6. Statistical analysis

Data are presented as mean ± standard deviation (SD) and range. Significance of difference between groups are assessed by pair t test or analysis of variance with post hoc paired comparisons according to the method of Tukey-Kramer as appropriate. Method agreement was assessed by concordance correlation and limits of agreement (LOA) analysis. Statistical analyses were performed using Medcalc version 22.016 (Medcalc Software Ltd, Ostend, Belgium).

3.1. Participant characteristics

Participant characteristics are presented in table 1. Babies were all born at term with a mean gestational age of 39.0 ± 1.6 weeks. Mean body length at time of measurement (mean age 8.3 weeks) was 55.4 cm with a mean body weight of 4.8 kg. Reference body composition was 3.91 kg FFM and 0.88 kg FM.

Table 1. Participant characteristics.

 Curve fitting method  Cole modelRegression model P valueNumber72 Sex ratio (M:F)41:31 Gestational age (weeks)38.9 ± 1.6  (33.7–42.0) Measurement age (weeks)8.3 ± 4.8  (0.6–18.7) Weight (kg)4.79 ± 1.10  (2.42–7.34) Heel to crown length (cm)55.4 ± 4.3  (46.0–63.0) Reference fat-free mass (kg)3.91 ± 0.72  (2.12–5.53) Reference fat mass (kg)0.88 ± 0.43  (0.07–1.98) Number of files analysed (n, %)63 (87%)72 (100%) b 0.001 R0 (ohm)734 ± 77701 ± 80 a 0.001 (567–949)(470–935)  R∞ (ohm)433 ± 96529 ± 86 † 0.001 (257–699)(316–751) %SEE1.79 ± 4.51.04 ± 1.16ns (0.2–34.8)(0.29–9.2) 

Abbreviations: R0 , resistance at zero frequency; R∞ , resistance at infinite frequency; %SEE, percentage standard error of the estimate. a Paired t test. b z test for proportions.

3.2. Data modelling

Deviation of measured data from the Cole model was commonly observed for most files which were visually selected for correction by Td compensation (figure 1(A)). Deviation of reactance from the theoretical semi-circular plot was observed to occur from frequencies as low as 30 kHz in some participant data. Only a minority (n = 12, 16.6%) of data files fitted the expected Cole model semi-circle with minimal requirement for Td correction (figure 1(B)). Overall, 87% of BIS files could be fitted to the graphical Cole model with a mean %SEE of 1.8% although the quality of fitting was wide with some files exhibiting greater than 30%SEE.

In contrast, 100% of data files were fitted by regression to the R-frequency plot (table 1 and figure 1(C)) with %SEE approximately half that observed for Cole model fitting with a maximum %SEE one-third (9.2%) of that seen for the Cole model.

3.3. Estimation of R0 and R∞

Estimated R0 values values were significantly different between the two methods of calculation (table 1) although the two sets of data were highly correlated (R2 = 0.94, P < 0.0001, supplementary data figure 1(A)). R∞ values were less well correlated with greater scatter of data (R2 = 0.56, P < 0.0001, supplementary data figure 1(B)) and again were significantly different (table 1). Mean R0 was 4.7% smaller when estimated from the resistance than for the Cole model whereas R∞ was 22% larger.

3.4. Prediction of body composition

The correlations between predicted FFM and reference FFM are presented in figures 2(A) and (B) for Cole model prediction and Resistance-based prediction respectively. Correlation (Pearson's r) was strongest for the resistance based approach (r = 0.80) compared to the Cole model-based prediction (r = 0.75); the respective concordance correlations were lower at 0.79 and 0.64 respectively indicating that the data did not lie on the line of identity. The respective limits of agreement analysis are presented in figures 2(C) and (D) respectively. Both methods exhibited small overall bias −0.15 and −0.12 kg for Cole model prediction and resistance regression prediction respectively. Two SD limits of agreement were relatively large, particularly for the Cole model predictions (±32.6%), compared to resistance egression predictions (25.7%). Prediction of FM was the inverse of FFM since FM is calculated as BW-FFM (supplementary data figure 2).

Figure 2. Comparison of predicted fat-free mass with measured reference fat-free mass.

Download figure:

Standard image High-resolution image

The use of BIS in newborns and infants has, to date, been problematic due primarily to difficulty in modelling impedance data to the conventional Cole model. The results of the present study have demonstrated that the alternative of fitting the resistance–frequency spectrum provides estimates R0 and R∞ with similar precision (as %SEE) to that seen for Cole modelling. Furthermore, these estimates of R0 and R∞ when applied to mixture theory to assess body composition provide predictions that are in closer agreement with reference measures than those obtained when using Cole model-derived R0 and R∞ .

The resistance–frequency modelling approach relies upon the assumption that unlike reactance, resistance is only slightly if at all by the hook effect. Evidence exists that support this assumption. Theory suggests that the hook effect is due to capacitive leakage at high frequency (Scharfetter et al 1998, Buendía 2013) and empirical support has been provided by Buendia et al (2010a, 2010b). Scharfetter et al has suggested that the hook effect may in part be mitigated by limiting curve fitting to only frequencies up to 500 kHz (Scharfetter et al 1998). This is the default setting when Cole modelling but was not adopted for resistance–frequency modelling since, as noted above, resistance is largely immune to parasitic capacitance effects. Furthermore, this strategy would have decreased the number of data points available for data modelling, particularly those on the pseudo-plateau region extrapolated to infinite frequency. In addition, Buendia et al have suggested that deviation may occur from as low as 40 kHz (Buendía et al 2010a, 2010b); an observation confirmed here. Visual inspection of spectra for the present data set supports this view underscoring the relatively poor performance of conventional Td correction in such cases.

The impact of inadequate compensation for high frequency deviation on prediction of body composition was clear. In 13% of participants it was not possible to estimate body composition while in the remainder it was inaccurately predicted with wide limits of agreement when based upon conventional Cole modelling. In contrast, resistance-based modelling was able to provide body composition estimates for all participants with greater accuracy. Although not a primary aim of this study, it is of interest to assess predictive accuracy of this approach with empirically-derived prediction based methods in this age group. Limits of agreement vary from study to study ranging from ±8 to 13% (Lingwood et al 2012, Tint et al 2016). In contrast, BIS methods generally perform less well with best performing LOA around ±20% (Ward et al 2022) comparable to the LOA of ±25% for resistance-based modelling found here. Notably, BIS may perform much worse with LOA up to ±35% observed in some studies. Accuracy of BIS improves as infants mature with LOA of ±11% being observed in older infants (3.5 y) (Lyons-Reid et al 2023).

A limitation of the present study was that mixture modelling prediction of body composition used resistivity coefficients determined from Cole modelling. This necessitated converting resistance-derived R0 , and R∞ to their Cole equivalents. While the regression equations used to perform conversion had excellent predictive performance for R0 predictive performance was only moderate for R∞ reflecting the scatter in data. Inevitably, this introduced inaccuracy in the predicted Cole-equivalent values and will have contributed to the relatively wide LOA in prediction of body composition. Ideally, resistivity coefficients derived from resistance modelling are required.

In conclusion, this study has demonstrated that where BIS data are compromised by capacitive leakage, observable as the hook effect in Cole plots, modelling of the resistance–frequency spectrum provides satisfactory estimates of R0 and R∞ . These may then be used to provide acceptable predictions of body composition comparable to those afforded by conventional BIS analysis.

The authors acknowledge the willingness of parents for consenting to participate in this study.

The data cannot be made publicly available upon publication because they contain sensitive personal information. The data that support the findings of this study are available upon reasonable request from the authors.

LCW: conceptualization, data curation, formal analysis, writing—original draft, and writing—review and editing. NC: data collection, curation and analysis, methodology, writing—original draft, and writing—review and editing. TR and PR funding acquisition, data collection, curation and analysis, methodology, writing—original draft, and writing—review and editing.

This research was supported, in part, by Grants Nos. 2015/03333–6 and 2019/07717–4 from Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP).

Author Ward provides consultancy services to ImpediMed Limited. ImpediMed Limited was not involved in the conception, design, execution, data analysis for this study or in the preparation of the manuscript. All other authors declare no individual conflict of interest or financial ties to disclose.

The study was approved by the Ethics Committee of the School of Public Health, of the University of São Paulo, registry CAAE 59787216.2.0000.5421.