Accurate representation of the electrode-electrolyte/tissue interface is critical for the development of computational models of neural stimulation that can be used to enhance the efficacy and safety of the electrode and stimulation protocol. Computational models of deep brain stimulation (DBS) provide a valuable means with which to understand the distribution of current and voltage in the tissue surrounding the electrode and are used both clinically and in research to predict the regions of neural tissue activated during stimulation. The strength and distribution of the electric field in the vicinity of the stimulation electrodes depends on the applied current or voltage, the properties of the electrode-tissue interface, which mediates the transition of electron flow in the electrode to ion flow in the tissue, and the electrical and geometrical properties of the surrounding tissues. At the electrode-tissue interface an electrical double layer is formed, comprised of the inner Helmholtz layer with adsorbed ions and solvent molecules and a more diffuse layer of solvated ions and solvent molecules [1, 2]. Charge carried by electrons at the electrode is converted to charge carried by ions in the tissue either through capacitive coupling, with charging and discharging of the electrical double layer, or through Faradaic reactions involving oxidation and reduction, representing non-Faradaic and Faradaic charge transfer respectively [3]. During stimulation there may also be a reduction in electrode impedance due to stimulation-induced changes in the electrode-tissue interface, including desorption of protein ions at the electrode surface [4].
At high levels of applied current or voltage, the electrode interface exhibits nonlinear behavior, with impedance decreasing due to the combined reduction in charge transfer resistance and increased double layer capacitance [2, 5, 6]. This is accompanied by an increase in the proportion of charge transferred through Faradaic processes [7]. Changes in electrode interface properties and the transition to Faradaic charge transfer, as electrode capacitance is shunted, result in a shift to the majority of charge being transferred through the resistive component of the interface, leading to reversible or irreversible chemical reactions, with the potential to cause undesirable tissue damage [8–10]. Under voltage-controlled stimulation, these changes in the electrode-tissue interface will also affect the voltage distribution in the surrounding tissue and consequently may influence neural activation. The results of previous in vivo experimental studies in cats suggest that the current linearity limit may lie within the operating range of clinical DBS and that the electrode-tissue interface may operate within the nonlinear regime during therapeutic stimulation [7]. This implies that the assumption that the DBS electrode is ideally polarizable may not always hold for clinically relevant stimulation parameters.
In the majority of computational models of DBS to-date, it is assumed that the stimulating electrode is partially or ideally polarized [11–13]. Under this assumption, the major part of the charge is injected through the non-Faradaic component with little, or negligible, charge transferred through the Faradic component and interface properties are independent of frequency and the overpotential between the electrode and the tissue [14, 15]. Thus, the electrode-tissue interface is typically simulated using an equivalent circuit with a capacitor or constant phase element in parallel with a charge transfer resistor [14, 16–18], neglecting the nonlinear and overpotential-dependent properties of the interface [19].
Based on experimental data from Richardot and McAdams [16], Cantrell and Troy incorporated non-linear interface properties of metal microelectrodes in a finite element model using a thin layer approximation including full overpotential-dependent formulations of both resistive and capacitive interfacial components [1]. Their results indicate that at low amplitudes of the applied voltage, the current density at both the electrode edge and tip is more uniform than that estimated without the electrode interface. Moreover, at higher voltage amplitudes, a reduction in impedance is observed, causing the current distribution to become nonuniform, emphasizing the need to operate stimulating electrodes at the lowest possible amplitudes [1]. Similarly using a thin layer approximation, Howell et al represented nonlinear dependence of the electrode interface in a DBS model as the series combination of a Helmholtz capacitance and diffusion capacitance fitted to in vitro and in vivo experimental data [20], in parallel with a charge transfer resistance estimated using the Butler–Volmer equation. Their results indicate that during voltage-controlled stimulation with standard DBS pulse parameters, the electrode interface can be considered as an ideal polarized electrode with a nonlinear capacitance. The charge transfer resistance, however, was assumed to be infinite which may influence the point at which the model transitions from the linear to nonlinear regime.
Nonlinearities in the behavior of the electrode interface during current-controlled stimulation have not yet been incorporated in neurostimulation models. Changes in the impedance of the electrode-tissue interface directly affect the distribution of the electric field and extent of neural activation during voltage-controlled stimulation. While electrode impedance would be expected to have a negligible effect on the activation of neurons under current-controlled stimulation, as the voltage distribution in the surrounding tissue remains unchanged [4, 18], activation overpotentials generated at the electrode interface may alter the electrochemical behavior which can have an important influence in determining the safety of the applied stimulation.
To address these questions, in this paper we implemented a nonlinear model of the electrode interface in silico representing in vitro and in vivo conditions based on rat DBS electrodes for both current and voltage-controlled stimulation. The model incorporated experimentally obtained values for the electrode interface and encapsulation tissue electrical properties [4]. The unknown potentials at the electrode interface were solved using the time harmonic quasi-static formulation of Maxwell's equations with an iterative approach. The transition between linear and nonlinear behavior of the electrode interface as the applied voltage or current was increased was examined using the current-overpotential curves, or stationary polarization curves, for different frequencies. Activation of rodent subthalamic nucleus (STN) collateral axons, hypothesised to be preferentially activated during DBS [21, 22], was simulated to examine the effect of the nonlinear interface on neural activation during voltage-controlled stimulation. Finally, the point of transition to the nonlinear regime during current-controlled stimulation was determined from the nonlinear polarization curves and the corresponding charge density and charge per phase were compared with the Shannon model for predicting tissue damage [23].
The relationship between the applied stimulation current or voltage and the nonlinear properties of the electrode interface of a platinum iridium electrode was examined in a model of the electrode in 0.9% saline and in a model of the rat brain. The electric field in the model of the rat brain was then coupled to a population of multicompartment neuron axon models representing branching axon collaterals within the STN to examine the effect of nonlinear electrode properties on the extent of neural activation [21, 24]. The electric field surrounding the DBS electrode was simulated using a 3D piecewise heterogeneous model [4]. For both current and voltage-controlled stimulation, the electrode interface was incorporated into the finite element model using a thin layer approximation [16, 17], with the constant phase element impedance and charge transfer resistance varying as a function of the activation overpotential in the nonlinear model.
2.1. Finite element model of DBS electrode under in vitro and in vivo conditionsA geometric model of concentric DBS electrodes was generated based on the SNEX-100 electrode (Microprobes for Life Science, Gaithersburg, USA) commonly used for preclinical rodent DBS studies. The electrode comprised an active platinum iridium contact (tip diameter 100 μm, active surface area 0.0784 mm2) and a stainless-steel reference contact (diameter 330 μm, length 0.25 mm, surface area 0.34 mm2). The stimulation electrode and reference contact were separated by 0.5 mm of polyimide tubing of diameter 140 μm.
To represent in vitro conditions, the concentric electrode model was placed at a depth of 1 cm in a cylindrical domain representing a plastic test tube, 2.6 cm diameter and 10 cm long, filled with 0.9% saline solution. To simulate in vivo conditions, the electrode was positioned in the STN of a heterogeneous rat brain model composed of cerebrospinal fluid, and grey and white matter. The model was created using image segmentation of the Waxholm Space atlas of the Sprague Dawley rat Brain [25]. The segmented masks of the different brain tissues were converted to a geometric model using the Simpleware ScanIP software (Synopsys, USA) as described in Evers et al [4]. The electrode was surrounded by 100 μm thick encapsulation tissue representing the glial scar formed during chronic electrode implantation [4].
The potential in the finite element models was estimated using the time harmonic electric-quasi static Laplace equation, where magnetic and wave propagation effects are assumed to be negligible [18, 26, 27],

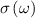 and
and  are electrical conductivity and relative permittivity,
are electrical conductivity and relative permittivity,  is angular frequency,
is angular frequency,  the permittivity of free space, and ϕ is the scalar potential. Maxwell's equation in this form considers the frequency-dependent (dispersive) conductivity and permittivity, where both conductivity and permittivity were described using the Cole–Cole equation representation of the dielectric properties of grey and white matter presented by Gabriel et al [28] and cerebrospinal fluid from De Geeter et al [29]. The conductivity and relative permittivity of the encapsulation tissue were based on the values estimated from in vivo experiments in Evers et al [4]. Conductivity and relative permittivity of the materials included in the models are presented in table 1.
the permittivity of free space, and ϕ is the scalar potential. Maxwell's equation in this form considers the frequency-dependent (dispersive) conductivity and permittivity, where both conductivity and permittivity were described using the Cole–Cole equation representation of the dielectric properties of grey and white matter presented by Gabriel et al [28] and cerebrospinal fluid from De Geeter et al [29]. The conductivity and relative permittivity of the encapsulation tissue were based on the values estimated from in vivo experiments in Evers et al [4]. Conductivity and relative permittivity of the materials included in the models are presented in table 1.
Table 1. Conductivity and relative permittivity values of the materials included in the in vivo and in vitro DBS models at 1 kHz.
MaterialConductivity (S/M)Relative permittivityGray mattera [28]0.0988164 060White mattera [28]0.062669 811Cerebrospinal fluid [29]2123Encapsulation tissuea [4]0.055 × 105Physiological saline [30]1.4143Pt-Ir contact [11]4.5 × 1061Steel contact [11]9 × 1051Polyimide [11]1 × 10−612.2. Linear representation of electrode interfaceThe electrode-tissue/electrode-electrolyte interface under linear conditions was represented using the equivalent circuit model proposed by Richardt and McAdams [14, 16]. The circuit model consists of the parallel combination of a constant phase element,  , and resistance,
, and resistance, 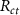 , with mathematical representation as given below
, with mathematical representation as given below



where  and
and  are constants denoting the magnitude of the impedance of the interface and the inhomogeneities on the electrode surface, respectively, R is the universal gas constant, F is Faraday's constant, temperature is given by T, n is the number of electrons per molecule,
are constants denoting the magnitude of the impedance of the interface and the inhomogeneities on the electrode surface, respectively, R is the universal gas constant, F is Faraday's constant, temperature is given by T, n is the number of electrons per molecule,  the exchange current density, i.e. the current at the equilibrium overpotential and
the exchange current density, i.e. the current at the equilibrium overpotential and  is total impedance of the electrical double layer interface (table 2). The constant phase element and charge transfer resistance of the electrode-tissue interface represent the non-Faradaic and Faradic charge transfer mechanisms, respectively, which are independent of frequency, activation overpotential, and the applied current or voltage amplitude in the linear model. The total admittance of the electrode interface calculated using equation (4) was incorporated into the in vitro and in vivo finite element models using a thin layer approximation [17, 18]. Due to the very thin nature of the electrical double layer, typically in the nanometer scale, mesh generation using finite element methods (FEMs) becomes computationally very expensive and can be challenging when integrating with larger structures. The thin layer approximation therefore provides a good compromise between the computational accuracy and ease of implementation [31]. Following a sensitivity analysis, an exchange current density of 6.41 × 10−4 A m−2 was assumed, based on the value used by Cantrall et al for platinum electrodes in physiological saline [17], adopted from McAdams and Jossinet [12].
is total impedance of the electrical double layer interface (table 2). The constant phase element and charge transfer resistance of the electrode-tissue interface represent the non-Faradaic and Faradic charge transfer mechanisms, respectively, which are independent of frequency, activation overpotential, and the applied current or voltage amplitude in the linear model. The total admittance of the electrode interface calculated using equation (4) was incorporated into the in vitro and in vivo finite element models using a thin layer approximation [17, 18]. Due to the very thin nature of the electrical double layer, typically in the nanometer scale, mesh generation using finite element methods (FEMs) becomes computationally very expensive and can be challenging when integrating with larger structures. The thin layer approximation therefore provides a good compromise between the computational accuracy and ease of implementation [31]. Following a sensitivity analysis, an exchange current density of 6.41 × 10−4 A m−2 was assumed, based on the value used by Cantrall et al for platinum electrodes in physiological saline [17], adopted from McAdams and Jossinet [12].
Table 2. Parameter values for linear and nonlinear electrode interface models.
K (Ω m2 s−β ) β RCt (Ω m2)Linear model [33]1.420.8523Nonlinear model [1] σ = 0.1552,
A = 1.42 Ωm2 s−β
σ = 0.1552,
A = 1.42 Ωm2 s−β


 = −3.736, b = 3.852,
c = 0.3697, d = −1.2112,
e = 0.9244
= −3.736, b = 3.852,
c = 0.3697, d = −1.2112,
e = 0.9244
![$}\left( \eta \right) = \frac}}nF\eta }}}} \right)}} - nF\eta }}}} \right)}}} \right]^}$](https://content.cld.iop.org/journals/1741-2552/21/1/016024/revision2/jnead2582ieqn9.gif?Expires=1709161204&Signature=d4EpqBGxB1FeHfBJXVwNU7jiPIXZkioi5m-sej0R-MXptfY1XFaGLEHbOFsjHnVxzFuxWOsCHn87j55otFJoJly0r~HrMaNIBZvBN8i9hL74cuZw3xQwfdseASECV4QYFuH32mTFDReAwdkvjpFFJz26o-UgDx8E2by2s9vcjF2wooq06OSuH8LgErxGusd-pib69MNCWnT9t2QDzN4uj5xlm-ilG0SwjT5YoIQruTLq~atoltZ42Y5ZT9cEXCvayj-ASJv1KZjvNVcHVbHXLaUZKGSbfUkbbOKjvOlmDLRqHeljgsUQr7ewtnpq1KroswyCGEvZrZ-HGiGWhIN2KA__&Key-Pair-Id=KL1D8TIY3N7T8)
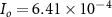 A m−2,
A m−2,  , T = 298 K
2.3. Nonlinear representation of electrode interface
, T = 298 K
2.3. Nonlinear representation of electrode interfaceA similar circuit model was used to incorporate nonlinear properties of the electrode interface using parameters based on the modeling and experimental study conducted by Richardot and McAdams for platinum electrodes immersed in NaCl solution [16]. In this condition both the constant phase element  and charge transfer resistance
and charge transfer resistance  parameters were estimated as a function of the activation overpotential,
parameters were estimated as a function of the activation overpotential,  :
:


where  and
and  are the overpotential-dependent form of the constants describing the magnitude of the impedance of the electrical double layer and the inhomogeneities on the electrode surface, respectively, and
are the overpotential-dependent form of the constants describing the magnitude of the impedance of the electrical double layer and the inhomogeneities on the electrode surface, respectively, and  and
and  are transfer coefficients. Equation (6) derives from the Butler–Volmer equation. Parameter values of
are transfer coefficients. Equation (6) derives from the Butler–Volmer equation. Parameter values of  A m−2,
A m−2, 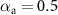 ,
,  , T = 298 K were assumed. The nonlinear constant phase element parameters were derived from the equations below as described by Cantrell et al [17], assuming that
, T = 298 K were assumed. The nonlinear constant phase element parameters were derived from the equations below as described by Cantrell et al [17], assuming that  and
and  are a function of the activation overpotential,
are a function of the activation overpotential,  .
.


σ = 0.1552,  = −3.736, b = 3.852, c = 0.3697, d = −1.2112, e = 0.9244 are coefficients determined through curve fitting of experimental data conducted by Richardot and McAdam [16]. A = 1.42 Ωm2 s-β
was experimentally estimated for the Pt-Ir SNEX-100 electrode in vitro [4]. The activation overpotential is defined as the potential difference between the metal electrode,
= −3.736, b = 3.852, c = 0.3697, d = −1.2112, e = 0.9244 are coefficients determined through curve fitting of experimental data conducted by Richardot and McAdam [16]. A = 1.42 Ωm2 s-β
was experimentally estimated for the Pt-Ir SNEX-100 electrode in vitro [4]. The activation overpotential is defined as the potential difference between the metal electrode,  , and the adjacent tissue or electrolyte,
, and the adjacent tissue or electrolyte,  , less the equilibrium overpotential
, less the equilibrium overpotential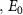 ,
,

It was assumed that the electrode is operating about the equilibrium overpotential [1] or that the equilibrium overpotential is equal to zero [20]. Equation (6), the Butler–Volmer equation describes the electrochemical kinematics under the assumption that the concentrations at the electrode are not substantially different to those within the bulk tissue or physiological saline and mass transfer phenomena can thus be neglected [32]. Consistent with this, post-mortem examination of the brain parenchyma surrounding implanted electrodes in patients [33] and rodents [4] have not shown signs of migration of electrode material into the tissue. Similar to the linear model, the total admittance of the electrical double layer was incorporated into the thin layer approximation. A summary of the linear and nonlinear electrode interface model parameters is presented in table 2. As the overpotential is a function of the potential at the electrode interface, which is itself a function of the electrode impedance, an iterative approach was used to solve for the electric potential in the tissue surrounding the electrode as described in section 2.6.
2.4. Finite element model2.4.1. Boundary conditionsIn the finite element model, the platinum iridium contact of the microelectrode core was assigned as the active terminal and the stainless-steel contact surface was assigned as ground, figure 1(B). Neumann boundary conditions were applied to the insulating parts of the electrode and the outer surface of the rat tissue in the in vivo model, figures 1(A) and (B). A point at the dorsal roots of the spinal nerves was defined as ground, figure 1(A). For the in vitro model, Neumann boundary conditions were applied to the outer surface of the cylindrical saline domain and insulating part of the electrode. For both linear and nonlinear interface models, the electrode interface was implemented using the thin layer approximation [1] on the active contact surface for both voltage and current-controlled stimulation. The intrinsic properties and thickness of the electrical double layer were represented through the total admittance calculated from the equivalent circuit parameters in equation (4) which were incorporated into equation (10).
Figure 1. Representation of the thin layer approximation at the electrode and boundary conditions for bipolar stimulation for (A) in vivo and (B) in vitro finite element models of the rat DBS electro
Comments (0)