The connectivity of the human brain is integral to cognitive capacity, can be an early marker for human disease, and underlies the fundamental functioning of the central nervous system (Ashburner et al 2004). However, measuring connectivity in vivo has proven problematic (Rowe 2010, Fiecas et al 2013, Andellini et al 2015). Functional magnetic resonance imaging (fMRI 6 ) of the brain measures the blood-oxygen-level-dependent (BOLD) signal and serves as an indirect measure of neural activity. The brain scan can be parcellated into neuroanatomical regions and the mean regional time series can be computed from the voxels in each region. By measuring temporal relationships between the mean BOLD signal from two or more regions of the brain, the underlying direct and indirect connectivity and communication within the brain can be probed. The connections between regions can then be used to represent the subject-specific connectome as a connectivity graph with each region represented as a node in the graph, while the edges between nodes are assigned an edge strength proportion to the pairwise regional connectivity.

Connectivity measures are calculated from fMRI using a measure of similarity or information transfer between the mean regional BOLD timeseries of a pair of regions. Connectivity metrics can be grouped into undirected functional connectivity (FC) metrics and directed effective connectivity (EC) metrics. Functional connectivity is defined as the temporal coincidence of spatially distant neurophysiological events (Ashburner et al 2004) and it has been used to characterize the human connectome in both health and disease (Cohen et al 2017, Smitha et al 2017). FC is traditionally calculated as the correlation or partial correlation between the regional timeseries. Meanwhile, effective connectivity is defined as the influence one neural system exerts over another (Ashburner et al 2004). Broadly, this is a model-dependent measure wherein the information transfer between mean regional timeseries is quantified from the goodness of fit of a model that predicts one of the timeseries from one or more of the other timeseries. Examples of EC measures include Granger causality (Granger 1969, Spencer et al 2018, Abidin et al 2019, Chockanathan et al 2019), dynamic causal modeling (Park et al 2018, Friston et al 2019), and structured equation modeling (SEM) (Rowe 2010), which have been widely deployed for connectome characterization. EC is inherently directional as it captures the direction of information flow over time (Bielczyk et al 2019). EC is model-dependent and requires more computation than FC but suppresses spurious indirect connections and identifies linkages that are potentially causal and not simply correlated.

Traditional FC and EC measures have several limitations, for which we propose new solutions. Common FC measures include Pearson's r, partial correlation, and spectral Granger causality (Ding et al 2006). Each of these methods measure a degree of linear association between two mean regional timeseries; however, the actual relationship between mean regional brain activity is nonlinear (Friston et al 2019). Therefore, we propose nonlinear machine learning models that measure FC while capturing such nonlinearities. Of the different EC measures, we focus on Granger causal (GC) methods as they are data-driven approaches that can be used when many neuroanatomical regions, N, are to be analyzed (e.g. N> 50). In modern fMRI connectivity analysis N is often a hundred or more. Alternative causal models, including dynamic causal models and SEMs, typically apply an exhaustive search over possible connectivity patterns, making analysis at this ROI granularity intractable for current compute hardware. Limiting the connectivity to a subset of the brain, such as intra-DMN connectivity, is often used as a workaround, but this restricts the portion of the brain under consideration and can miss important interactions (Rowe 2010, Friston et al 2019). Granger causal methods have limitations as well but these, we hypothesize, are surmountable, including: model selection procedures, regularization, scalability (the traditional GC method requires fitting O(N2) sub-models where N is the number of regions under analysis), an inability to capture nonlinear interactions, and the absence of the incorporation of prior knowledge of brain architecture (Ashburner et al 2004). To address these limitations, we propose two measures of effective connectivity. The first measure which we call Machine-Learning FC (), uses a nonlinear machine learning model to quantify nonlinear pairwise timeseries associations. Our method is more scalable because the number of required models to fit scales as O(N). Our second measure, which we call Structurally-Projected Granger Causality (), reformulates Granger causal connectivity in two ways. First, we regularize the connectivity computation using a structural connectivity (SC) prior derived from diffusion MRI. Streamline tractography is performed on diffusion MRI from the Human Connectome Project (HCP) and a streamline atlas is generated (Yeh et al 2018). The log of the number of streamlines connecting regions is used as a measure of pairwise structural connectivity. This is used to regularize the functional interactions inferred between regional timeseries via a tradeoff between the raw functional data interactivity and fiber bundle connectivity. As actual neural communication occurs through physical connections, this constraint is a natural choice of a prior to guide brain FC (Allen and Weylandt 2019, Huang and Ding 2016, Dillon et al 2017, Manning et al 2018, Maglanoc et al 2020). The second way we reformulate Granger causal connectivity is to perform dimensionality reduction. Calculating the connectivity in a low dimensional space affords several advantages including: simplifying model optimization as there are fewer weights to tune and providing further regularization to stabilize fMRI interpretation and increase reproducibility. This dimensionality reduction is achieved by projecting the mean regional timeseries into a low dimensional space informed by the streamline SC prior. Each of our proposed measures is evaluated for reproducibility and the ability to predict cognitive and physiological traits of the HCP participants in our study.

A connectivity measure should produce a similar connectivity matrix for a given individual across repeat fMRI scans that are acquired within a short window of time. Therefore, we evaluated the proposed FC and EC measures reproducibility across four repeated fMRI scans of each individual in our HCP-derived dataset. A reproducible measure better characterizes an individual's connectivity fingerprint and is therefore more useful to capture true differences between individuals (Waller et al 2017, Noble et al 2019). Reproducibility is necessary, but insufficient to show that the proposed measures have validity; therefore we also measure the predictive power of each FC and EC metric in three relevant domains: a purely physiological domain predicting mean arterial pressure, a purely cognitive domain measuring fluid intelligence, and a combined physiologic and cognitive domain measuring stress. These were chosen as representative targets of interest of researchers and clinicians interested in predictions for physiology (e.g. stroke, aging), cognition (e.g. memory, PTSD), or a combination of the two (e.g. stress, neurodegeneration) for diagnoses and treatment. Measures that are both reproducible and have consistently high predictive power across multiple tasks are significantly more useful as candidate biomarkers (Termenon et al 2016, Waller et al 2017, Noble et al 2017a, 2017b). We postulate that a measure that is both more reproducible and predictive is a better representation of true underlying neural patterns than alternative measures. The contributions of this work are: (1) the development of a new functional connectivity metric ( ML.FC ) and a new effective connectivity metric ( ML.EC ) that efficiently capture nonlinear associations between brain regions, (2) the development of a new effective connectivity metric ( SP.GC ) that incorporates a SC prior while efficiently measuring associations across all brain regions in a low dimensional space, (3) a quantitative comparison of the proposed measures to traditional measures of connectivity in terms of reproducibility and the power to predictive traits of individual subjects. Finally, (4) we recommend individual measures that hold the most potential to advance the study of human brain connectivity in health and disease based on the quantitative comparison.

2.1. Methods2.1.1. Proposed machine learning-based functional connectivity ( measures)

Characterizing brain connectivity to better understand both health and disease is a complex process requiring measuring both linear and nonlinear aspects of information transfer between brain regions. Classical means of performing this characterization include the use of Pearson's r, partial correlation, and spectral Granger causality. (For definitions of classical measures of FC, see supplemental section 9.1.2.) Central to this premise, we propose the construction of a machine learning model to calculate functional connectivity, an approach we denote as . This model predicts the activity, , at a given node by using the information present at all other nodes (brain regions) at any given time, . As illustrated in equation (1), we use a nonlinear model to predict the activity at region at time from all other regions under analysis except region

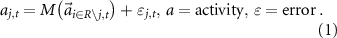
This model simultaneously learns the association between all other nodes' activity and the target node . The weight assigned to each covariate quantifies the amount of information the model is using from that node to predict the target node , which is a putative measure of the connectivity between each node and . This draws on the theory of Granger causality which uses the coefficients of a bilinear model to quantify instantaneous information transfer (i.e. the relationship between signals at a fixed single time ) by predicting the activity of node at time, , from other nodes, , with a linear model (Ding et al 2006, Luo et al 2013).

For resting state fMRI, we want to derive a measure of functional connectivity between every set of nodes, resulting in a functional connectivity (FC) matrix. Our procedure using the covariate weights from the predictive model populates one row of the FC matrix at a time. If we repeat the process for each region, we fill the entire FC matrix by fitting models. The choice of model determines what associations we can detect between regions from the predicted covariate weights, which enables granular modeling control compared to previous attempts that use only one model (Murugesan et al 2020). In this work we allow to be any of the following models: (1) the extremely random trees model (ERTs), (2) nonlinear radial basis function kernel support-vector machine regressor (SVM), (3) Extreme Gradient Boosting forest models (XGB) (Chen et al 2016). The ERT was chosen because it produces high performance across a wide domain of machine learning applications (Feczko et al 2018, Mellema et al 2022). The SVM was chosen because it is a high-performing machine learning model which has a more directly interpretable and explicit weights than the ERT (Deshpande et al 2010, Arora et al 2018, Mellema et al 2022). The XGB was chosen because it tends to have higher performance than the ERT, and handles multicollinearity from repeated data sub-sampling, which we hypothesize will better handle correlated regional information than the ERT.

For each proposed model, we use the following model fitting approach. First, the mean timeseries per region is standardized with a mean of 0 and unit variance. Then, a model is fit to predict regional activity at node at every time from other all other nodes at each time . Then, a measure of feature weight or importance is extracted from the model for each nodal covariate . We repeat this for each node to fully populate an asymmetric FC matrix. The asymmetric matrix is then symmetrized by averaging itself with its transpose. Feature importance is calculated from the Gini importance for the ERT, the covariate weight for the SVM, and the Gini importance weighted by number of samples routed through the decision node for the XGBoost model. The XGBoost model was fit with a group-level hyperparameter search. The ERT and SVM models did not benefit from this search; their default parameters were already optimal. The hyperparameter evaluations were done on HCP data NOT used in training, validation, or testing. For additional model fitting details see supplemental section 9.1.3. In order to evaluate the relative benefits of each proposed ML.FC measure, we test each FC measure's reproducibility and evaluate its predictive power by using it to infer three individual traits of interest (see section 2.4).

2.1.2. Background of effective connectivity

In addition to functional connectivity, brain connectivity can be quantified with measures of time-delayed information transfer, which we denote as effective connectivity measures. Effective connectivity can be quantified in numerous ways: multivariate Granger-causal (GC) scores (Spencer et al 2018, Abidin et al 2019, Chockanathan et al 2019), bilinear GC modeling (Luo et al 2013), and other measures of directed neural influence (Bielczyk et al 2019). This paper builds new measures from the mathematical foundation of Granger causal modeling. GC measures define a directed edge by quantifying how the past history of activity signal B from a particular brain region informs the future activity of signal A, from another brain region. In neuroimaging, signal B is said to be Granger causal of signal A if a model to predict the future of A given all past information from all regions' signals including B is more accurate than a model that does not include B. The degree of causality is called the GC score (Granger 1969). To generate a Granger causal effective connectivity matrix, the Granger score between the regional time courses from each pair of regions is calculated using the GC algorithm (algorithm 1). A full model, f, is fit to predict activity in region i at time t from the past history of all regions. Then, a reduced model f' is fit to predict the same activity at time t from the past history of all regions except j. The EC score is the log of the ratio of the standard deviation of the residuals of the full and reduced models. By using a linear model f, a baseline measure of effective connectivity can be calculated. The linear models with which we calculate the GC score include: an unpenalized multivariate autoregressive (MVAR) model denoted , an elastic MVAR model with a small L1 and L2 penalty (L1= L2= λ = 0.1) denoted , and an elastic MVAR model with a large L1 and L2 penalty (λ =10) denoted . These regularization amounts were chosen empirically to be representative of strong and weak regularization. The timeseries is tested for significant autoregression with the Augmented Dickey Fuller test and any significant autoregression is removed prior to model fitting. Lag values of 1-5 times repetition time (TR) were tested and the model using the lag with the lowest Akaike information criterion was selected independently for each regional model.

Algorithm 1. GC algorithm. This algorithm describes the steps by which one calculates an effective connectivity matrix from a neural timeseries using a standard Granger-causal approach. = neural activity matrix of size by , where and where . = number of timepoints. = max lag. = timeseries predictor function. = secondary indexer from to . = effective connectivity matrix of size , indexed by and . = reduced timeseries predictor function without region . = standard deviation.

Inputs: X ti, (i ∈ [1,N], t ∈ [1,T]),τ, f;Input timeseries with number of regions N, number of timepoints T, max lag τ, timeseries predictor f; Output: E;Output effective connectivity matrix E; for i:=1 to N do Full model fit